Helping Patients Now and Later
March 17, 2020

Peter Norwood, PhD Candidate
March 17, 2020

Peter Norwood, PhD Candidate
What is the goal of a clinical trial? Is it to aid sick patients that sign up for the trial? Is it to collect the best possible information so we can treat future patients? Can we simultaneously achieve both goals?
Traditionally, the goal of clinical trials is to gain valuable information to confidently recommend effective treatment to future patients. Often, simple randomization (e.g., 50% to treatment, 50% to placebo) is the gold standard to achieve this goal. However, is there a cost to simple randomization?
Imagine a clinical trial designed to ultimately include 1000 patients (typically, patients enter in batches, not all at once). At a certain point in time, our trial has 500 patients who were randomized 50/50 to the treatment and placebo and have completed the trial. Based on these 500 patients, we are confident that the treatment is effective. What should we do next? Continue to randomize 50% of the future patients to the placebo? Give all future patients the treatment? Something in between these two?
This is one problem adaptive randomization attempts to solve: we wish to simultaneously improve in-trial patient outcomes while maintaining—or even improving—the information we would have achieved through simple randomization. We want to carefully balance efficacy and information gain.
Let’s consider some situations. Assume a certain number of patients have gone through the trial, and based off of that, we can estimate metrics for efficacy and information gain. Now, we have a decision to make: we can give a new patient either treatment 1 or treatment 0. For the following scenarios, which treatment should we administer?
Scenario One
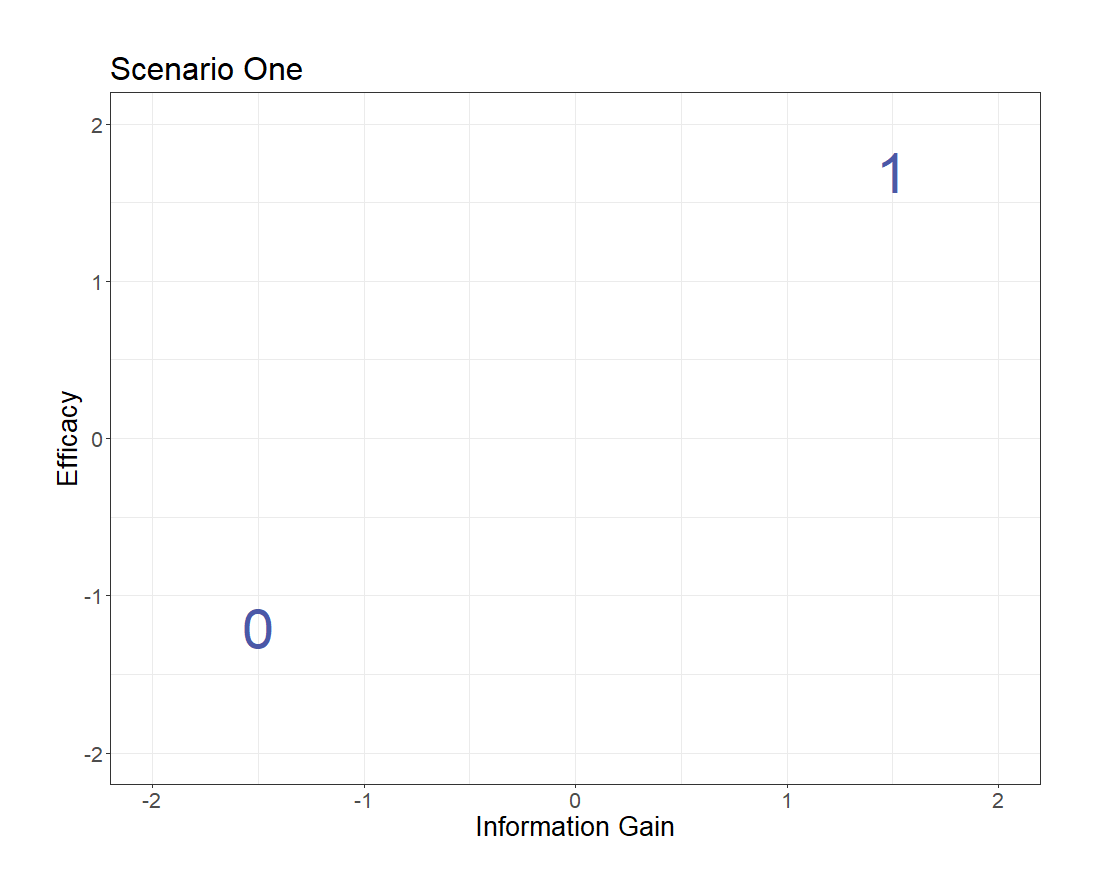
Here, the answer is obvious—
treatment 1 is superior to treatment 0.
We estimate that treatment 1 is both better for the patient and gives us more information.
Now consider another scenario:
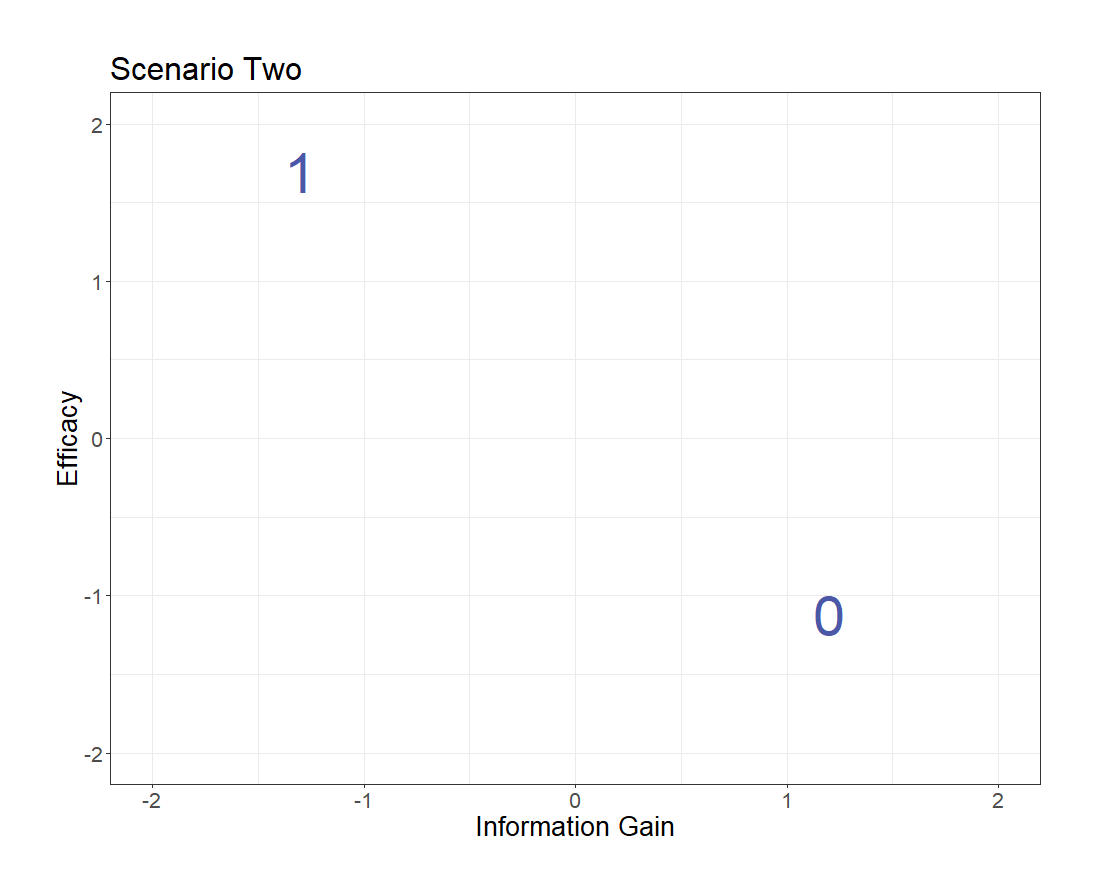
Now, the answer is not so obvious.
Treatment 1 is better for the patient, but treatment 0 may be more valuable down the line.
Perhaps picking at random is the better choice.
Now consider the next five patients to enter the trial. With two treatment options each, we have 2^5 different options to choose from.
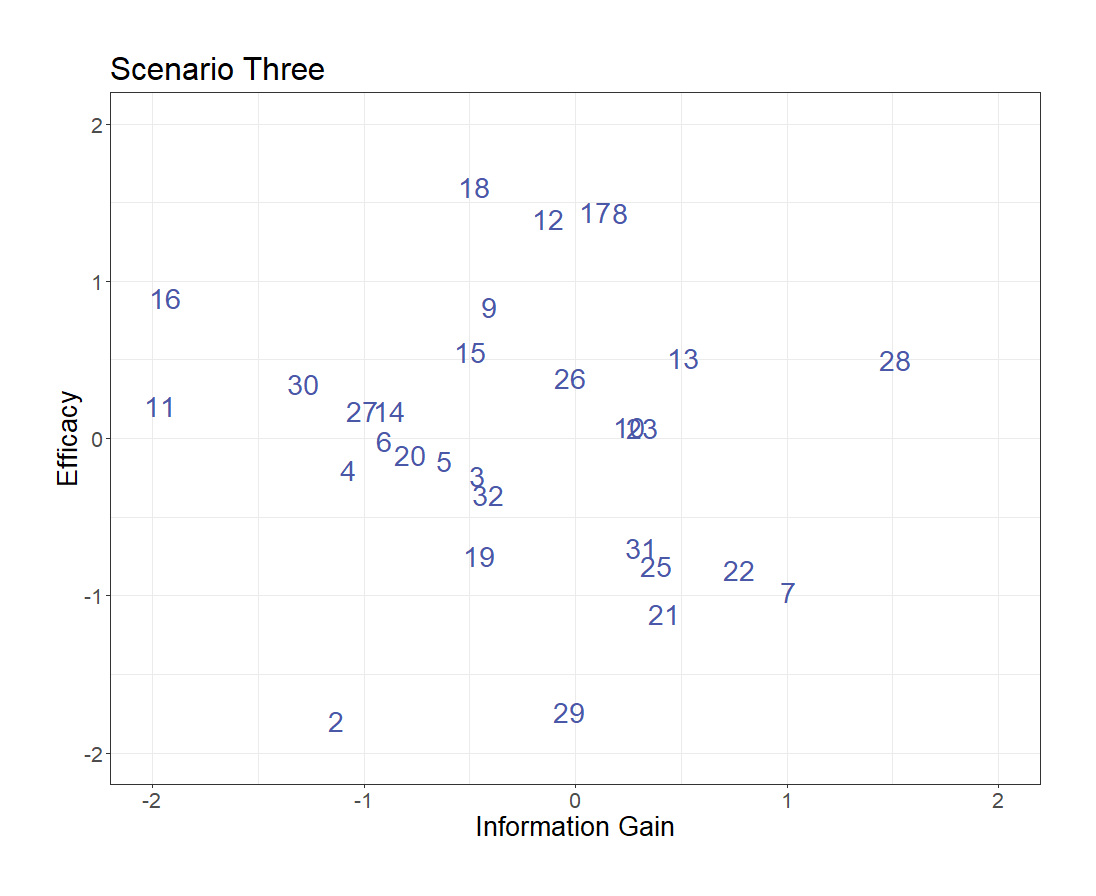
It gets even trickier—
28 gives the best information gain, 18 offers the top efficacy, and 17 and 8 both seem like a nice blend.
So another problem arises: how do we pick which treatment combinations offer some value?
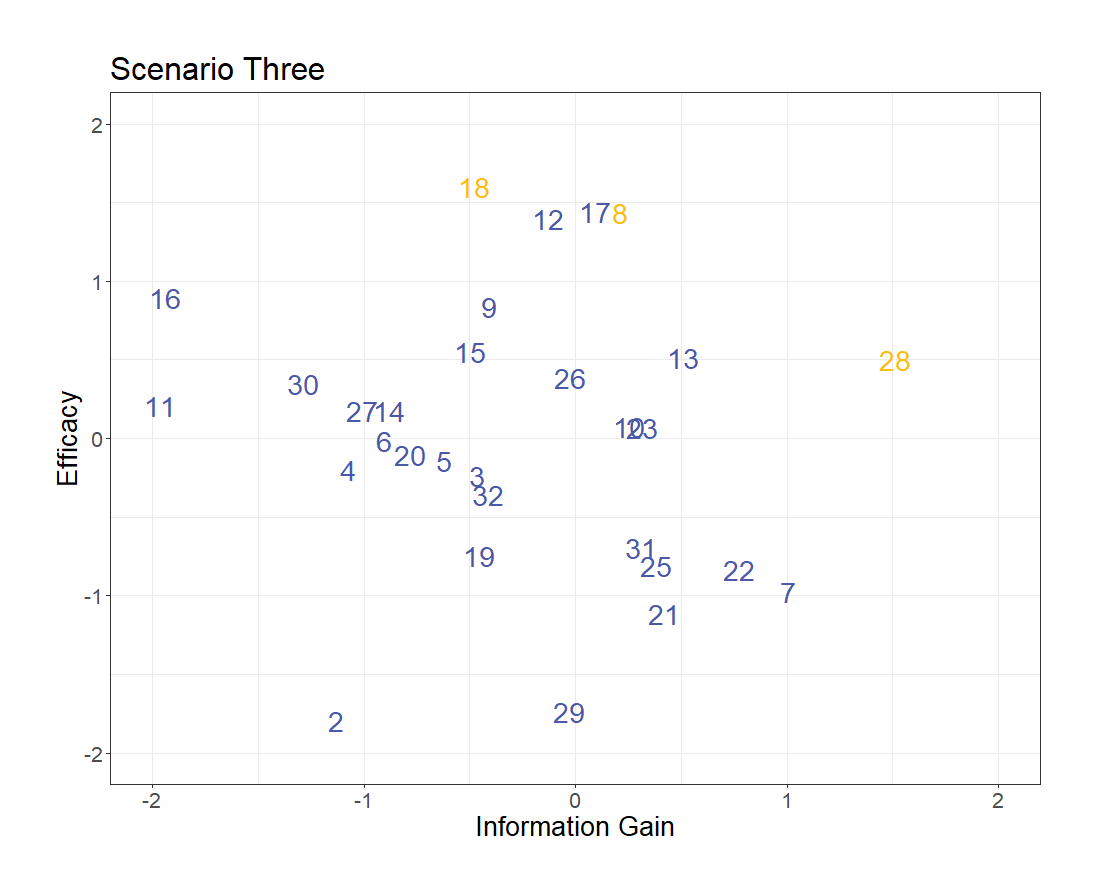
One option is to pick treatment combinations that maximize a convex combination of our efficacy and information gain metrics. Doing this yields the yellow points as valuable treatment combinations:
Overall this seems like a reasonable criteria. We could also consider the uncertainty in our estimates of the efficacy and information gain metrics to include other points—perhaps 12 and 17 could be included.
After coming up with a list of valuable treatment options, the next step is to randomize between them. Should we simply randomize between all of them? Should we start by favoring information gain then moving towards efficacy?
As statisticians, our goal is to study these questions so we can ultimately find the proper solution to a given problem. We develop strategies, understand their mathematical properties, and simulate them over and over to see how they would perform in a real-world setting. Ultimately, clinical trials will be conducted, patients will be treated, and future treatment regimes will be decided. Our job is to provide clinicians the proper information to understand the tradeoffs of different strategies so they can choose wisely based on their specific interests.
Peter is a PhD candidate whose research interests include causal inference, dynamic treatment regimes, and statistical learning. This is Peter’s first blog post, so we thought we’d take this opportunity to ask him a probing question to get to know him a bit better.
If you had to make a sequel to a movie (with or without the studios permission), a billion dollars in your budget (mostly to deal with lawsuits), and had to make it statistics related, which movie would you pick and what would it be about?
I would make a twist of The Departed (spoiler alert). The story wouldn't change but there would be a deep dive into the probability that Matt Damon and Leonardo DiCaprio simultaneously:
We wouldn't need to use one billion dollars to make many new scenes, but we would need to properly compensate the statistician who calculates these complicated probabilities for us. Naturally, the statistician is me.