The Art of Cheating
April 10, 2020

Cole Manschot, PhD Candidate
April 10, 2020

Cole Manschot, PhD Candidate
Cheaters win. It’s an inherent advantage gained by the willing. The risk takers. The daredevils. The payoffs can be massive depending on the level and potential gain, but so can the risk. Don’t believe me? Look up Cambridge Analytica, Russia Olympic Ban, or the 2012 Harvard Cheating Scandal. So, should we cheat? How do we decide when to cheat?
Should we cheat?
If you are only concerned with yourself and not others, you may consider cheating acceptable when the outcome from cheating is more favorable than the outcome from not cheating. If you are concerned with how your actions might be perceived or affect others, you may determine limits where you deem cheating okay if kept within those limits.
If you value honesty and integrity above potential gains, you would act without ever cheating. However, you would also likely lose to cheaters and be left with only your pride to console you. Unfortunately, pride doesn’t put food on the table or keep the lights on.
This is one problem adaptive randomization attempts to solve: we wish to simultaneously improve in-trial patient outcomes while maintaining—or even improving—the information we would have achieved through simple randomization. We want to carefully balance efficacy and information gain.
You may also consider cheating okay so long as no one else is hurt by your actions. Like if you are playing solitaire and allow yourself to re-do certain moves.
All of these can be described through what we call a utility function. A utility function assigns a value to what we prefer and our proclivity towards such. For instance, someone who values their needs above others would have a low utility gain from others succeeding unless the person themselves also succeeded whereas one who values others much greater than themselves could have a high utility when other succeed even if they themselves are in dire straits. At the end of the day, we are all just agents trying to maximize our own utility function.
How do we decide when to cheat?
According to my ethics professor, approximately 46% of graduate students in the United States have admitted to misconduct in some capacity [1]. Assuming that this is not by mistake, many people are considering weighing the risk against the rewards. Most institutions have very strict policies meant to deter students from these behaviors, but only 2% of reported investigations into cheating allegations result in a punishment.
As statisticians, our goal is to study these questions so we can ultimately find the proper solution to a given problem. We develop strategies, understand their mathematical properties, and simulate them over and over to see how they would perform in a real-world setting. Ultimately, clinical trials will be conducted, patients will be treated, and future treatment regimes will be decided. Our job is to provide clinicians the proper information to understand the tradeoffs of different strategies so they can choose wisely based on their specific interests.
So, do we cheat? Let’s find out!
*Disclaimer: Even though there seems to be minimal risk and potentially high payoffs, I do not recommend graduate students cheat. This is not advice from a doctor. Encouraging everyone to cheat is not ethically correct.
Scenario:
Dwigt, a hypothetical student, only cares about getting his PhD and starting to make more money. More specifically, Dwigt is concerned with how much money he will make five years from now.
If Dwigt cheats and does not get caught, he will be able to finish his doctorate in one year and get a high paying job because his falsified work amazes those in his field. If he cheats and does get caught and punished, he will be shunned by both the members of the lab he works in and by industry because of his lack of morality and take a low paying job as a mechanical turk at the end of the first year. If Dwigt does not cheat, it will take him two years to finish his PhD and he will make a respectable wage at a decent job, but nowhere near what he would make if he cheats.
We can illustrate this process as a decision tree!
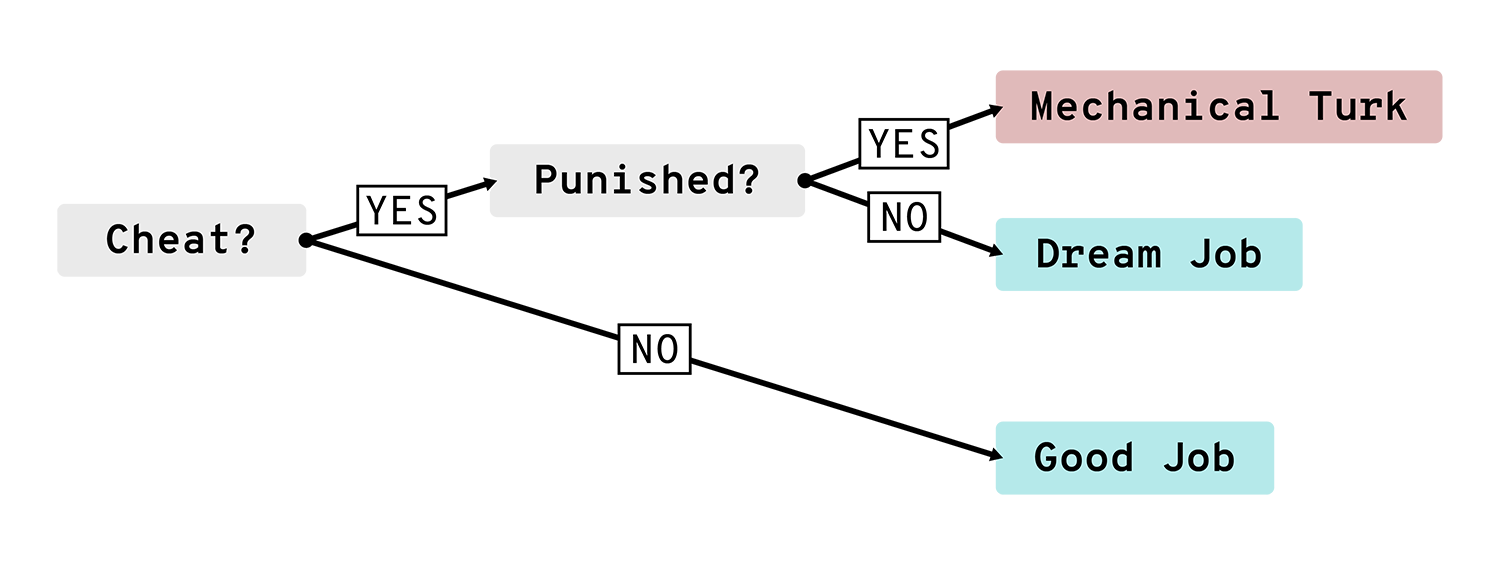
So finally, what should Dwigt do? Let’s assume that Dwigt is typical of graduate students and use the standard rates of cheating and getting caught. Then the probability of Dwigt “getting” each of the jobs is:
| Job | Chance of Outcome |
|---|---|
| Mechanical Turk | 0.92% |
| Dream Job | 45.08% |
| Good Job | 54% |
We know Dwigt loves cash money, so we want to figure out what salary differences should be to give Dwigt reason to cheat. Dwigt, hypothetically speaking, would cheat if his expected cheating salary is greater than his expected not cheating salary. Or mathematically, Dwigt will cheat if:

Dwigt makes minimum wage as a mechanical turk in North Carolina so his salary would be $7.25 per hour then. After some math, Dwigt will cheat if his dream job will pay him 2% more than the good job minus 14.5 cents per hour.
If you’re like me, that’s a fine equation but I have no context… so here is some!
We can see that for even good paying jobs, the difference in cost for Dwigt, who cares only for himself, need be less than $3000 for him to chose to cheat!
| Good Salary | Dream Salary Needed |
|---|---|
| $100,000.00 | $101,733.06 |
| $110,000.00 | $111,937.14 |
| $120,000.00 | $122,141.22 |
| $130,000.00 | $132,345.31 |
| $140,000.00 | $142,549.39 |
| $150,000.00 | $152,753.47 |
This seems like there is minimal risk for cheating in graduate school, and that is assuming that if you are caught you make $7.25 an hour! These differences decrease as the pay of the ‘lesser’ job increases! Based on these differences, no wonder so many graduate students have admitted to cheating! There is relatively little incentive to be honest for one whose utility is gained only through self.
References
[1] Comstock, Gary; 14 January 2020, PHI 816 Lecture at NC State University.
Cole is a graduate student in Laber Labs. He is interested in decision making and sports science but also thinks that a better framework should exist to discourage unethical behavior. This article is meant to illustrate the faults of the current system. He is a big fan of The Office and wants to include subtle references in his blog posts so that some day he may meet John Krasinski and Jenna Fischer.
Suppose you are in charge of playing music for the lab throughout and entire workday, but you can only choose one artist. What artist do you choose and why?
With any choice of lab music, I think there needs to be a balance between continuity and variety of style. The artist needs to create a common sustained sound while not entering into monotonous drones and repetition. An ideal artist would have at most each song played twice. Transitions are key to the continuity aspect. Music may become distracting if the differences in the compositions (or songs) is too dynamic or volatile, but the songs themselves should be dynamic and exhibit a wide range. Lyrics, if any, should not be distracting or distasteful so as to respect my fellow lab mates. With all this in mind, I would chose the works of Antonin Dvorak who encapsulates the optimal solution to all these constraints.