Outcome Regression Estimator
The outcome regression estimator of the optimal treatment regime, \(\widehat{d}^{opt}_{Q,1}(h_{1})\), is characterized by the estimated rule
\[ \widehat{d}^{opt}_{Q,1}(h_{1}) = \underset{a_{1} \in \mathcal{A}_{1}}{\arg\!\max}~Q_{1}(h_{1},a_{1};\widehat{\beta}_{1}), \] where \(Q_{1}(h_{1},a_{1};\beta_{1})\) is a model for \(Q(h_{1},a_{1}) = E(Y|H_{1} = h_{1}, A_{1} = a_{1})\) and \(\widehat{\beta}_{1}\) is a suitably obtained estimator of \(\beta_{1}\).
The value, \(\mathcal{V}(d^{opt})\) can be estimated by the sample average
\[ \widehat{\mathcal{V}}_{Q}(d^{opt}) = n^{-1} \sum_{i=1}^n \underset{a_{1} \in \mathcal{A}_{1}}{\max}~Q_{1}(H_{1i},a_{1}; \widehat{\beta}_{1}). \]
A general implementation of the regression estimator is provided in
utils::str(object = DynTxRegime::qLearn)function (..., moMain, moCont, data, response, txName, fSet = NULL, iter = 0L, verbose = TRUE) We briefly describe the input arguments for DynTxRegime::
| Input Argument | Description |
|---|---|
| \(\dots\) | Ignored; included only to require named inputs. |
| moMain | A “modelObj” object. The modeling object for the \(\nu_{1}(h_{1}; \phi_{1})\) component of \(Q_{1}(h_{1},a_{1};\beta_{1})\). |
| moCont | A “modelObj” object. The modeling object for the \(\text{C}_{1}(h_{1}; \psi_{1})\) component of \(Q_{1}(h_{1},a_{1};\beta_{1})\). |
| data | A “data.frame” object. The covariate history and the treatment received. |
| response | A “numeric” vector. The outcome of interest, where larger values are better. |
| txName | A “character” object. The column header of data corresponding to the treatment variable. |
| fSet | A “function”. A user defined function specifying treatment or model subset structure. |
| iter | An “integer” object. The maximum number of iterations for iterative algorithm. |
| verbose | A “logical” object. If TRUE progress information is printed to screen. |
Methods implemented in DynTxRegime break the outcome model into two components: a main effects component and a contrasts component. For example, for binary treatments, \(Q_{1}(h_{1}, a_{1}; \beta_{1})\) can be written as
\[ Q_{1}(h_{1}, a_{1}; \beta_{1})= \nu_{1}(h_{1}; \phi_{1}) + a_{1} \text{C}_{1}(h_{1}; \psi_{1}), \]
where \(\beta_{1} = (\phi^{\intercal}_{1}, \psi^{\intercal}_{1})^{\intercal}\). Here, \(\nu_{1}(h_{1}; \phi_{1})\) comprises the terms of the outcome regression model that are independent of treatment (so called “main effects” or “common effects”), and \(\text{C}_{1}(h_{1}; \psi_{1})\) comprises the terms of the model that interact with treatment (so called “contrasts”). Input arguments moMain and moCont specify \(\nu_{1}(h_{1}; \phi_{1})\) and \(\text{C}_{1}(h_{1}; \psi_{1})\), respectively.
In the examples provided in this chapter, the two components of \(Q_{1}(h_{1}, a_{1}; \beta_{1})\) are both linear models, the parameters of which are estimated using stats::
The value object returned by DynTxRegime::
| Slot Name | Description |
|---|---|
| @step | For single decision point analyses, this will always be 1. |
| @analysis@outcome | The outcome regression analysis. |
| @analysis@txInfo | The treatment information. |
| @analysis@call | The unevaluated function call. |
| @analysis@optimal | The estimated value, \(Q\)-functions, and optimal treatment for the training data. |
There are several methods available for objects of this class that assist with model diagnostics, the exploration of training set results, and the estimation of optimal treatments for future patients. We explore these methods in the Methods section.
We continue to consider the three outcome regression models introduced in Chapter 2, which represent a range of model (mis)specification. For brevity, we discuss the function call to DynTxRegime::
Inputs moMain and moCont are modeling objects specifying the outcome regression step. To illustrate, we will use the true outcome regression model
\[ Q^{3}_{1}(h_{1},a_{1};\beta_{1}) = \beta_{10} + \beta_{11} \text{Ch} + \beta_{12} \text{K} + a_{1}~(\beta_{13} + \beta_{14} \text{Ch} + \beta_{15} \text{K}), \]
which is defined as a modeling objects as follows
q3Main <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')q3Cont <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')Note that the formula in the contrast component does not contain the treatment variable; it contains only the covariates that interact with the treatment.
Both components of the outcome regression model are of the same class, and the models for each decision point should be fit as a single combined object. Thus, the iterative algorithm is not required, and iter should keep its default value, 0.
As for all methods discussed in this chapter: the “data.frame” containing the baseline covariates and treatment received is data set dataSBP, the treatment is contained in column $A of dataSBP, and the outcome of interest is the change in systolic blood pressure measured six months after treatment, \(y = \text{SBP0} - \text{SBP6}\), which is already defined in our R environment.
Circumstances under which this input would be utilized are not represented by the data set generated for illustration in this chapter.
The optimal treatment regime, \(\widehat{d}_{Q,1}^{opt}(h_{1})\), is estimated as follows.
QL3 <- DynTxRegime::qLearn(moMain = q3Main,
moCont = q3Cont,
data = dataSBP,
response = y,
txName = 'A',
fSet = NULL,
verbose = TRUE)First step of the Q-Learning Algorithm.
Outcome regression.
Combined outcome regression model: ~ Ch+K + A + A:(Ch+K) .
Regression analysis for Combined:
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) Ch K A Ch:A K:A
-15.6048 -0.2035 12.2849 -61.0979 0.5048 -6.6099
Recommended Treatments:
0 1
238 762
Estimated value: 13.21562 Above, we opted to set verbose to TRUE to highlight some of the information that should be verified by a user. Notice the following:
- The first line of the verbose output indicates that the selected value estimator is the first step of the Q-learning algorithm. As will be discussed in later chapters, the outcome regression estimator is equivalent to the first step of the Q-learning algorithm introduced in Chapter 5.
Users should verify that the intended estimator was used. - The information provided for the outcome regression is not defined within DynTxRegime::
qLearn() , but is specified by the statistical method selected to obtain parameter estimates; in this example it is defined by stats::lm() .
Users should verify that the model was correctly interpreted by the software and that there are no warnings or messages reported by the regression method. - Finally, a tabled summary of the recommended treatments and the estimated value for the training data are shown.
The sum of the elements of the table should be the number of individuals in the training data. If it is not, the data set is likely not complete; method implementation in DynTxRegime require complete data sets.
The first step of the post-analysis should always be model diagnostics. DynTxRegime comes with several tools to assist in this task. However, we have explored the outcome regression models previously and will skip that step here. Available model diagnostic tools are described under the Methods tab.
For the regression estimator, the form of the outcome regression model dictates the class of regimes under consideration. For model \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) the regime is of the form
\[ \widehat{d}_{Q,1}^{opt}(H_{1}) = \text{I}(\widehat{\beta}_{13} + \widehat{\beta}_{14}~\text{Ch} + \widehat{\beta}_{15} \text{K} > 0). \]
The parameter estimates, \(\widehat{\beta}\) can be retrieved using DynTxRegime::
DynTxRegime::coef(object = QL3)$outcome
$outcome$Combined
(Intercept) Ch K A Ch:A K:A
-15.6048448 -0.2034722 12.2848519 -61.0979087 0.5048157 -6.6098761 and thus \(\widehat{d}^{opt}_{Q,1}(h_{1}) = \text{I}\) (-61.10 + 0.50 Ch - 6.61 K > 0) or equivalently \(\widehat{d}^{opt}_{Q,1}(h_{1}) = \text{I}\)(-0.99 + 0.01 Ch - 0.11 K > 0), where we have required \(|\eta_{1}| = 1\).
There are several methods available for the returned object that assist with model diagnostics, the exploration of training set results, and the estimation of optimal treatments for future patients. A complete description of these methods can be found under the Methods tab.
In the table below, we show the estimated value under each of the outcome regression models considered and the total number of individuals in the training data recommended to each treatment.
| \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) | |
| \(\widehat{\mathcal{V}}_{Q}(d^{opt})\) | 14.26 | 13.16 | 13.22 |
| \((n_{\widehat{d} = 0}, n_{\widehat{d} = 1})\) | (0, 1000) | (238, 762) | (238, 762) |
We illustrate the methods available for objects of class “QLearn” by considering the following analysis:
q3Main <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')q3Cont <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')result <- DynTxRegime::qLearn(moMain = q3Main,
moCont = q3Cont,
data = dataSBP,
response = y,
txName = 'A',
iter = 0L,
verbose = FALSE)| Function | Description |
|---|---|
| Call(name, …) | Retrieve the unevaluated call to the statistical method. |
| coef(object, …) | Retrieve estimated parameters of outcome model(s). |
| DTRstep(object) | Print description of method used to estimate the treatment regime and value. |
| estimator(x, …) | Retrieve the estimated value of the estimated optimal treatment regime for the training data set. |
| fitObject(object, …) | Retrieve the regression analysis object(s) without the modelObj framework. |
| optTx(x, …) | Retrieve the estimated optimal treatment regime and decision functions for the training data. |
| optTx(x, newdata, …) | Predict the optimal treatment regime for new patient(s). |
| outcome(object, …) | Retrieve the regression analysis for the outcome regression step. |
| plot(x, suppress = FALSE, …) | Generate diagnostic plots for the regression object (input suppress = TRUE suppresses title changes indicating regression step.). |
| print(x, …) | Print main results. |
| show(object) | Show main results. |
| summary(object, …) | Retrieve summary information from regression analyses. |
The unevaluated call to the statistical method can be retrieved as follows
DynTxRegime::Call(name = result)DynTxRegime::qLearn(moMain = q3Main, moCont = q3Cont, data = dataSBP,
response = y, txName = "A", iter = 0L, verbose = FALSE)The returned object can be used to re-call the analysis with modified inputs.
For example, to complete the analysis with a different outcome regression model requires only the following code.
q3Main <- modelObj::buildModelObj(model = ~ (K + Ch + Cr),
solver.method = 'lm',
predict.method = 'predict.lm')
eval(expr = DynTxRegime::Call(name = result))Q-Learning: step 1
Outcome Regression Analysis
Combined
Call:
lm(formula = YinternalY ~ K + Ch + Cr + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) K Ch Cr A Ch:A K:A
-15.4733 12.2874 -0.2035 -0.1761 -61.0865 0.5048 -6.6132
Recommended Treatments:
0 1
238 762
Estimated value: 13.21521 This function provides a reminder of the analysis used to obtain the object.
DynTxRegime::DTRstep(object = result)Q-Learning: step 1 The
DynTxRegime::summary(object = result)$outcome
$outcome$Combined
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Residuals:
Min 1Q Median 3Q Max
-9.0371 -1.9376 0.0051 2.0127 9.6452
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -15.604845 1.636349 -9.536 <2e-16 ***
Ch -0.203472 0.002987 -68.116 <2e-16 ***
K 12.284852 0.358393 34.278 <2e-16 ***
A -61.097909 2.456637 -24.871 <2e-16 ***
Ch:A 0.504816 0.004422 114.168 <2e-16 ***
K:A -6.609876 0.538386 -12.277 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.925 on 994 degrees of freedom
Multiple R-squared: 0.961, Adjusted R-squared: 0.9608
F-statistic: 4897 on 5 and 994 DF, p-value: < 2.2e-16
$optTx
0 1
238 762
$value
[1] 13.21562Though the required regression analysis is performed within the function, users should perform diagnostics to ensure that the posited model is suitable. DynTxRegime includes limited functionality for such tasks.
For most R regression methods, the following functions are defined.
The estimated parameters of the regression model(s) can be retrieved using DynTxRegime::
DynTxRegime::coef(object = result)$outcome
$outcome$Combined
(Intercept) Ch K A Ch:A K:A
-15.6048448 -0.2034722 12.2848519 -61.0979087 0.5048157 -6.6098761 If defined by the regression methods, standard diagnostic plots can be generated using DynTxRegime::
graphics::par(mfrow = c(2,2))
DynTxRegime::plot(x = result)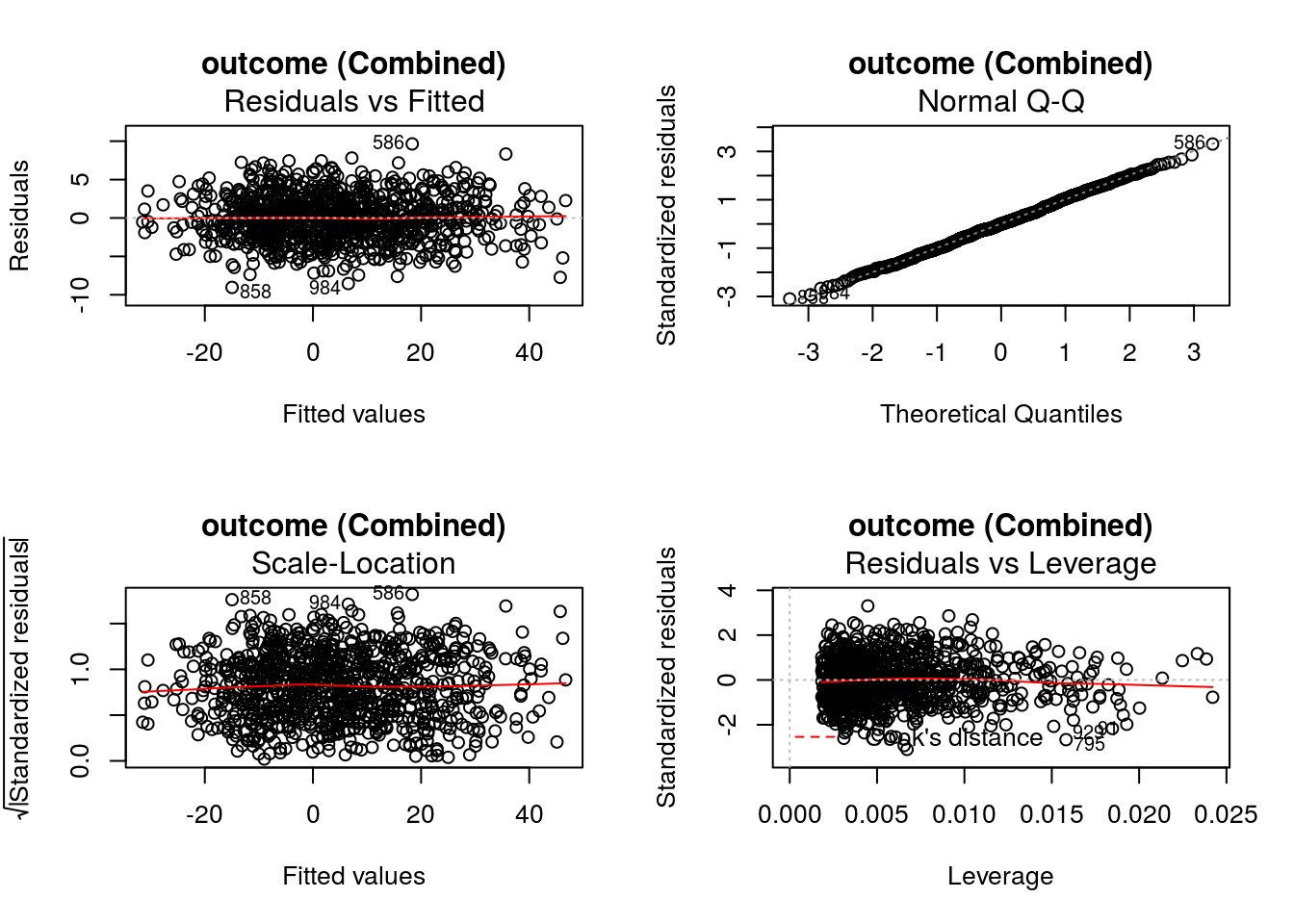
The value of input variable suppress determines if the plot titles are concatenated with an identifier of the regression analysis being plotted. For example, below we plot the Residuals vs Fitted for the outcome regression with and without the title concatenation.
graphics::par(mfrow = c(1,2))
DynTxRegime::plot(x = result, which = 1)
DynTxRegime::plot(x = result, suppress = TRUE, which = 1)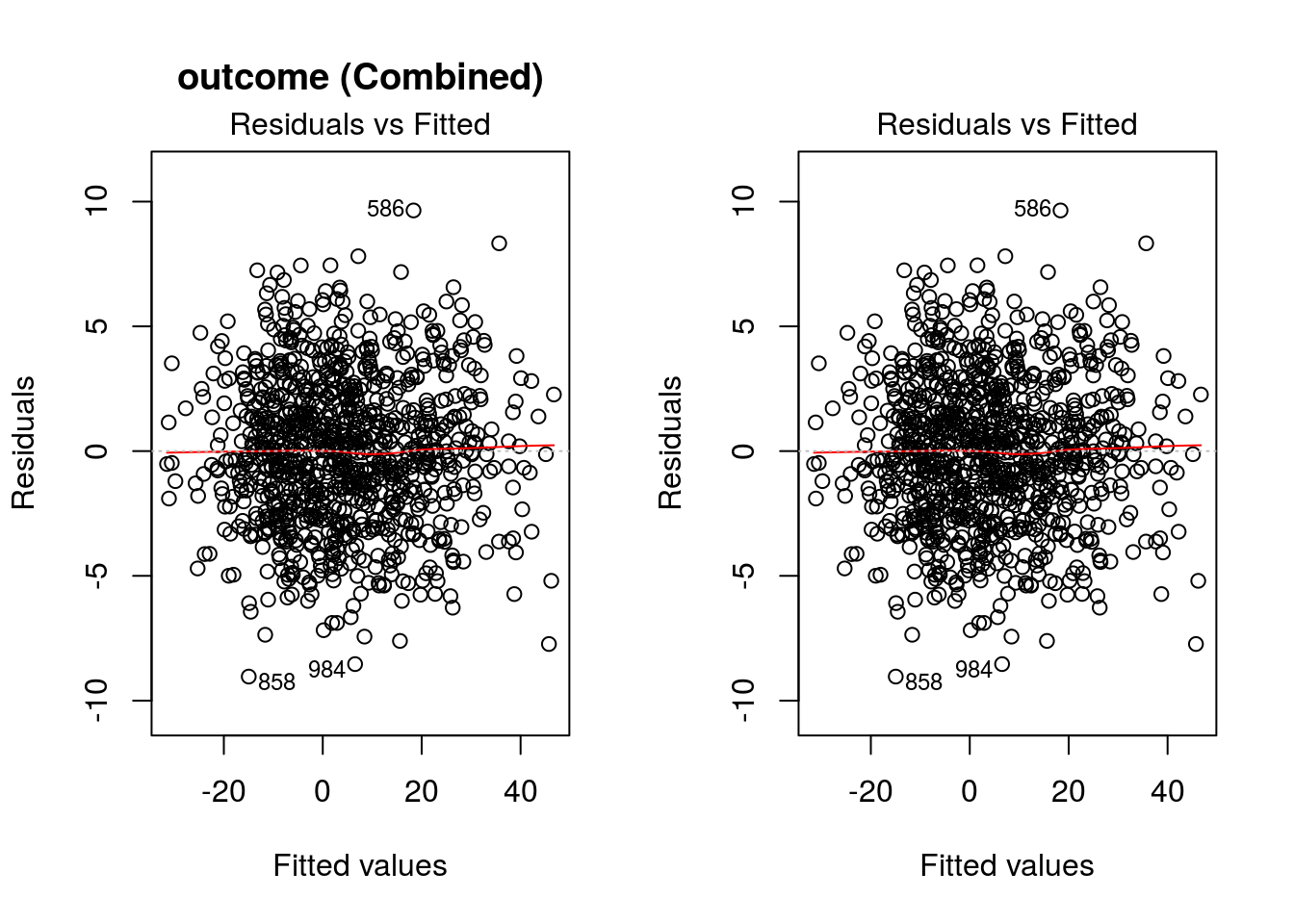
If there are additional diagnostic tools defined for a regression method used in the analysis but not implemented in DynTxRegime, the value object returned by the regression method can be extracted using function DynTxRegime::
fitObj <- DynTxRegime::fitObject(object = result)
fitObj$outcome
$outcome$Combined
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) Ch K A Ch:A K:A
-15.6048 -0.2035 12.2849 -61.0979 0.5048 -6.6099 As for DynTxRegime::
is(object = fitObj$outcome$Combined)[1] "lm" "oldClass"As such, these objects can be passed to any tool defined for these classes. For example, the methods available for the object returned by the outcome regression are
utils::methods(class = is(object = fitObj$outcome$Combined)[1L]) [1] add1 alias anova case.names coerce confint cooks.distance deviance
[9] dfbeta dfbetas drop1 dummy.coef effects extractAIC family formula
[17] hatvalues influence initialize kappa labels logLik model.frame model.matrix
[25] nobs plot predict print proj qr residuals rstandard
[33] rstudent show simulate slotsFromS3 summary variable.names vcov
see '?methods' for accessing help and source codeSo, to plot the residuals
graphics::plot(x = residuals(object = fitObj$outcome$Combined))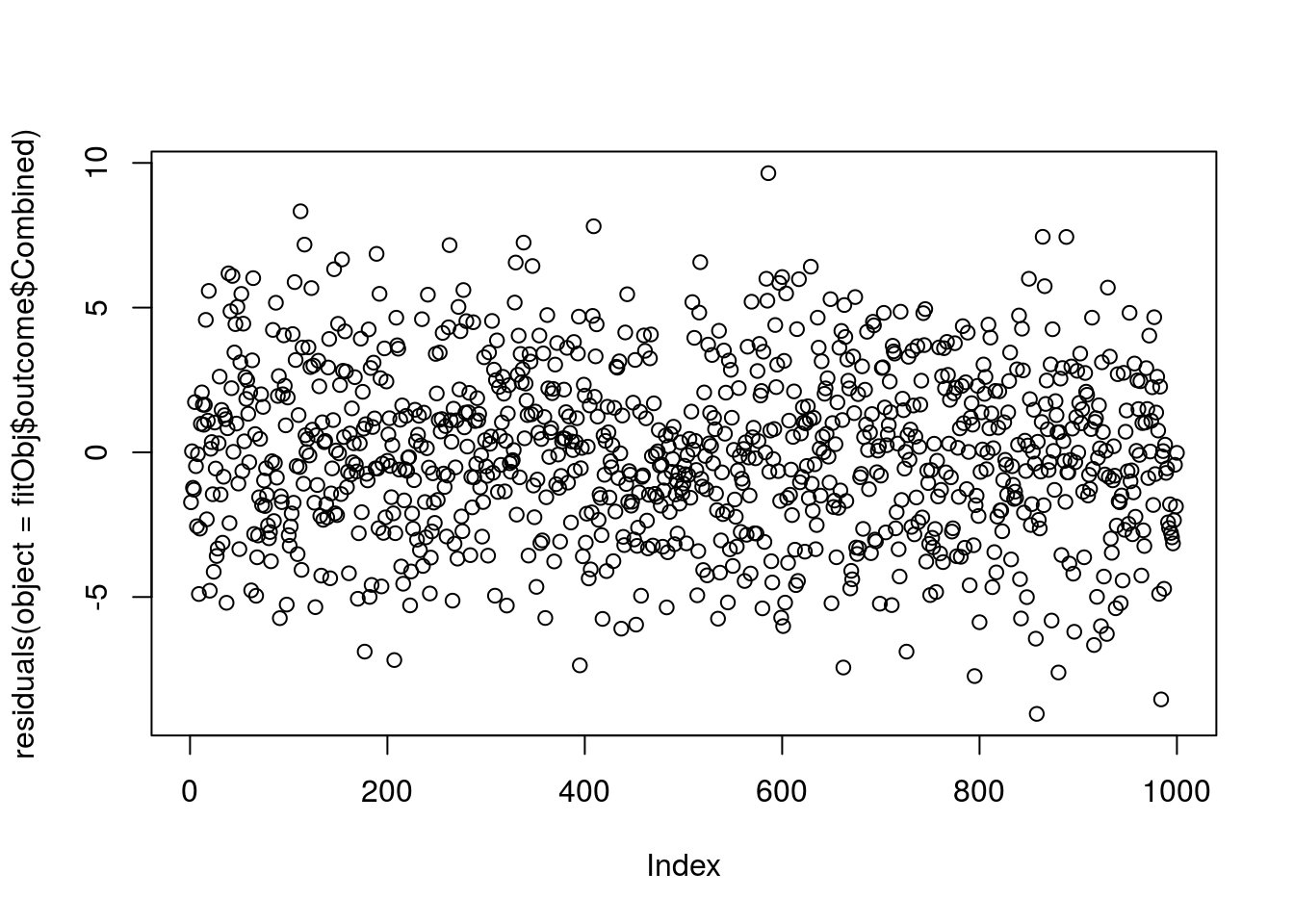
Or, to retrieve the variance-covariance matrix of the parameters
stats::vcov(object = fitObj$outcome$Combined) (Intercept) Ch K A Ch:A K:A
(Intercept) 2.677636513 -1.845763e-03 -5.448948e-01 -2.677636513 1.845763e-03 5.448948e-01
Ch -0.001845763 8.922966e-06 1.833617e-05 0.001845763 -8.922966e-06 -1.833617e-05
K -0.544894783 1.833617e-05 1.284459e-01 0.544894783 -1.833617e-05 -1.284459e-01
A -2.677636513 1.845763e-03 5.448948e-01 6.035065761 -4.114621e-03 -1.218665e+00
Ch:A 0.001845763 -8.922966e-06 -1.833617e-05 -0.004114621 1.955124e-05 -4.548556e-06
K:A 0.544894783 -1.833617e-05 -1.284459e-01 -1.218665266 -4.548556e-06 2.898598e-01The methods DynTxRegime::
DynTxRegime::outcome(object = result)$Combined
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) Ch K A Ch:A K:A
-15.6048 -0.2035 12.2849 -61.0979 0.5048 -6.6099 Once satisfied that the postulated model is suitable, the estimated optimal treatment, the estimated \(Q\)-functions, and the estimated value for the dataset used for the analysis can be retrieved.
Function DynTxRegime::
DynTxRegime::optTx(x = result)$optimalTx
[1] 0 0 1 1 1 1 1 0 1 1 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1
[60] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 0 1
[119] 0 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1
[178] 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 0 1 1 1 0 0 1 0 1 1 0 1 1 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1
[237] 1 1 1 0 1 0 1 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1
[296] 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 1 0 1 1 1
[355] 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 0 0 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1
[414] 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1
[473] 0 1 1 1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 1 0 0 1 1 0 1 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0
[532] 0 1 1 1 0 1 1 1 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 0 1
[591] 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 0 1 1 1 1 1 0 1 1 0 0 0 1 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 1 1
[650] 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1
[709] 1 1 1 1 1 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 1 0 1 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1 0 0 0 1 1 1 1
[768] 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 0 0 1 1 0 1 0 1 1 1 1 0 1 0 1 0 0
[827] 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 1 0 0 1 1 0 1 1 1
[886] 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 1 0 1 1 1 1 1 1 0 1 0 1 0 0 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
[945] 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 1 0 1 0 0 0 1 1 1 1
$decisionFunc
0 1
[1,] -4.27317742 -5.1700387
[2,] 2.96295528 0.8214458
[3,] -11.29296760 5.2263119
[4,] -25.70888388 36.1239344
[5,] -21.97021401 16.2655940
[6,] -23.20374219 20.4793479
[7,] -9.44641376 7.2653376
[8,] 7.06544119 -7.6412514
[9,] -12.20337418 20.8959777
[10,] -1.36335002 9.6156208
[11,] -6.98683428 15.5571428
[12,] -13.31481905 24.9289255
[13,] -16.93418996 18.3547783
[14,] 7.04752786 -19.5491786
[15,] 10.35908138 -19.6798261
[16,] -29.91832410 30.4236833
[17,] 3.31390098 -4.4720896
[18,] 0.90527716 -3.2917949
[19,] 0.83658339 -5.5769504
[20,] -0.21886282 3.1468458
[21,] -7.12178792 -0.9512297
[22,] -9.35493890 -2.4177027
[23,] 4.44830219 -1.3783617
[24,] -23.87259127 28.6305915
[25,] -19.37585611 21.9709002
[26,] -15.46153816 18.5606637
[27,] -5.41766462 1.2987364
[28,] 2.32714853 6.5368621
[29,] 2.22541244 6.6875338
[30,] -6.61554136 10.2334730
[31,] -3.65249966 3.4582994
[32,] -22.19646729 28.5351334
[33,] 6.12442617 -1.4738199
[34,] -7.44212519 13.8445399
[35,] -12.28476305 21.0165151
[36,] -13.14456443 7.9685378
[37,] -26.06487258 46.1987213
[38,] -7.83133144 7.2602825
[39,] 7.43169111 -8.1836697
[40,] 0.44494326 -0.2231463
[41,] -9.87353011 26.9930305
[42,] -13.10873776 31.7843921
[43,] 2.90452274 8.0686589
[44,] 7.05778908 -10.0168100
[45,] -19.65810805 29.5495912
[46,] -7.42943008 11.4388470
[47,] -3.91440437 11.0068560
[48,] 2.33723452 -3.0256408
[49,] -12.92074503 7.6370599
[50,] -14.65530155 14.9797311
[51,] -22.11003542 23.6333445
[52,] -11.47348345 12.6543311
[53,] -3.56589256 17.6513821
[54,] -18.98664986 28.5551576
[55,] 1.62003890 2.8103129
[56,] -0.59276486 1.3137055
[57,] 1.64803823 5.1557371
[58,] -15.49214660 9.0584294
[59,] -11.33105292 12.4433907
[60,] -8.03984662 12.3428775
[61,] -19.65045594 31.9251497
[62,] -8.23062369 10.2385281
[63,] -12.17798396 16.0845919
[64,] -5.01819714 17.4153623
[65,] -4.17891821 11.3986025
[66,] -14.39583072 19.3692360
[67,] -7.04283294 10.8662944
[68,] -20.53808141 35.6266197
[69,] -8.12645371 -1.8502052
[70,] -8.74939013 20.5543898
[71,] -10.46359943 27.8669266
[72,] -4.00605447 1.5950248
[73,] -2.17984785 3.6641848
[74,] -19.53359085 17.4307236
[75,] -6.02547204 9.3595769
[76,] 1.32752574 0.8566352
[77,] -22.44828601 26.5211870
[78,] 5.47070608 -7.6663307
[79,] -7.47273363 4.3423057
[80,] -9.13859638 13.9701324
[81,] 10.75333063 -17.8768202
[82,] -11.17836117 21.7648188
[83,] -9.25807058 21.3077485
[84,] -4.22969864 21.0213742
[85,] 4.37456543 1.1177342
[86,] -18.44492708 25.3659716
[87,] -13.35812260 17.8323842
[88,] -5.12497623 22.3472855
[89,] -26.44399284 30.0519610
[90,] -5.35401385 8.3651433
[91,] -12.96369812 38.7302616
[92,] -5.48374927 6.1703909
[93,] -20.27878581 20.9212531
[94,] -10.00587464 17.6414680
[95,] -11.04114887 7.2402583
[96,] -8.91234310 1.7005930
[97,] -5.93138806 6.8333466
[98,] -2.73948396 -5.0545564
[99,] -11.77869171 13.1063464
[100,] -5.99486360 18.8618111
[101,] -16.93905773 42.2309013
[102,] -2.43931869 -0.7253201
[103,] -8.88938677 8.8272687
[104,] 2.91460874 -1.4938441
[105,] -5.30323342 -1.2576283
[106,] 0.11938777 0.2590033
[107,] -9.18955204 4.4980325
[108,] -30.52613153 38.4845238
[109,] -16.26012265 24.5171548
[110,] -14.28644252 21.5941228
[111,] 4.11005160 1.5094808
[112,] -25.40367561 35.6719192
[113,] -22.85766426 39.0619355
[114,] -6.62075959 -4.0801470
[115,] -7.60490293 14.0856147
[116,] -5.55487692 15.8232969
[117,] 12.40910739 -17.9421439
[118,] -16.16603867 21.9909244
[119,] -0.45798644 -1.2727935
[120,] -13.20038786 22.3725609
[121,] -7.77272367 19.1079410
[122,] -7.06057104 18.0532387
[123,] -11.67434651 20.1124846
[124,] -16.58063514 20.2180529
[125,] -2.86643504 19.0023727
[126,] 4.74081535 0.5753159
[127,] -2.65044298 -2.7995352
[128,] 2.30419220 -0.5898136
[129,] -11.87034181 3.6945152
[130,] -16.16360479 10.0528630
[131,] -5.70252567 1.7206172
[132,] -14.69338687 22.1968098
[133,] -7.83133144 7.2602825
[134,] 14.96277086 -12.1765690
[135,] -15.65718300 40.3324372
[136,] -15.56570813 30.6493969
[137,] -18.65083314 37.6053766
[138,] -12.20841718 25.6772292
[139,] 14.25061823 -11.1218668
[140,] 4.62395027 15.0697421
[141,] -14.46452448 17.0840805
[142,] -15.84309230 14.3519648
[143,] -2.57896487 25.7373019
[144,] -14.44417726 17.0539462
[145,] 3.88605697 -17.2539129
[146,] -11.32600992 7.6621392
[147,] -0.34598913 8.1089033
[148,] -10.31369202 10.9366732
[149,] 5.32062345 -9.8309488
[150,] -6.44006851 7.5867053
[151,] -9.07494562 21.0365394
[152,] -0.83693147 1.6753177
[153,] 2.44157973 3.9804974
[154,] -10.66463773 16.2302086
[155,] -10.81715425 26.0036520
[156,] 5.47331520 -0.5095207
[157,] -15.26815197 27.8218231
[158,] -3.11321077 12.2071749
[159,] -29.79624080 30.2428772
[160,] -27.16623146 40.6691662
[161,] -18.99430197 26.1795991
[162,] -14.75199464 10.3491514
[163,] -9.23268036 16.4963627
[164,] 5.89295466 -3.5179006
[165,] -15.65474911 28.3943757
[166,] -25.67584155 33.6881072
[167,] -3.59650100 8.1491478
[168,] -7.15726413 13.4226590
[169,] 4.66203559 7.8526634
[170,] -3.93996982 -3.2766297
[171,] -16.20412400 29.2080032
[172,] 4.68985969 -8.8967840
[173,] -15.92691506 26.4105637
[174,] 0.06843211 -9.2130966
[175,] -8.53078896 5.9092919
[176,] -9.23789859 2.1827426
[177,] -0.97936200 1.8862582
[178,] -7.97115285 14.6280330
[179,] -5.87034641 6.7429435
[180,] -19.37585611 21.9709002
[181,] -12.52127755 23.7536859
[182,] -19.00438796 35.7421020
[183,] -18.91291309 26.0590617
[184,] 1.58195358 10.0273916
[185,] -30.80594958 34.1251533
[186,] 9.90135659 -9.4543674
[187,] -11.17070906 24.1403774
[188,] -7.61516415 4.5532461
[189,] 8.82295404 -7.8572469
[190,] -13.74211063 25.5617469
[191,] -7.37847442 20.9109469
[192,] -5.87538941 11.5241950
[193,] -11.56252443 10.3993100
[194,] -6.36633175 5.0906093
[195,] -6.61049836 5.4522215
[196,] -0.21625371 10.3036558
[197,] 0.40929182 -4.9441291
[198,] -13.74732886 11.2481268
[199,] -0.23155793 5.5525387
[200,] -9.70570937 21.9707042
[201,] 8.61704798 4.3821581
[202,] 4.82220422 0.4547785
[203,] -15.52762281 23.4323182
[204,] 15.55023106 -20.2072752
[205,] -8.24592791 5.4874110
[206,] -3.76675562 25.1095356
[207,] 0.17782031 -6.9882098
[208,] -7.20561068 11.1073692
[209,] -7.65064036 18.9271349
[210,] 1.48508525 -13.6980597
[211,] 9.42067547 -6.3555845
[212,] 13.59689814 -17.3143776
[213,] -9.12590128 11.5644395
[214,] -0.49607176 5.9442852
[215,] -16.62132958 20.2783216
[216,] 2.54053147 -22.4218559
[217,] -9.08259773 18.6609808
[218,] -9.41841444 9.6107618
[219,] -3.26068429 17.1993668
[220,] -22.52967489 26.6417244
[221,] -10.81211125 21.2224005
[222,] -9.83544479 19.7759517
[223,] -7.32769399 11.2881753
[224,] -22.88322970 24.7784498
[225,] -9.88379134 17.4606619
[226,] -12.92074503 7.6370599
[227,] -16.66967613 17.9630317
[228,] -1.47030434 -4.5473275
[229,] -9.88118222 24.6174719
[230,] -8.98103687 -0.5845625
[231,] -8.85634445 6.3914414
[232,] -11.63887030 5.7385959
[233,] -3.61684822 8.1792822
[234,] 17.85711880 -21.2368982
[235,] 3.40050808 9.7209930
[236,] -6.51641438 2.9259912
[237,] 1.63030012 12.3426815
[238,] -10.28308358 20.4389074
[239,] -3.45407047 7.9382074
[240,] 13.32734131 -12.1413796
[241,] -7.61516415 4.5532461
[242,] 11.52652491 -19.0219255
[243,] -6.12216513 4.7289972
[244,] 24.63796059 -16.9580166
[245,] -15.16398200 15.7330898
[246,] -11.27505426 17.1342391
[247,] -3.26329340 10.0425568
[248,] -21.67265785 13.4380202
[249,] 8.59913464 -7.5257691
[250,] -25.14438000 20.9665526
[251,] -5.95677828 11.6447324
[252,] -18.11693771 12.9457605
[253,] -20.18209272 25.5518328
[254,] -5.72026377 8.9075616
[255,] -31.14924317 41.7942472
[256,] -3.12608110 -4.4820037
[257,] -3.77440773 22.7339770
[258,] -16.80184543 27.7063408
[259,] 13.09343592 -2.2473989
[260,] 3.90901330 -10.1272372
[261,] -0.77084682 -3.1963368
[262,] 14.68051892 -4.5978781
[263,] -9.15894360 14.0002667
[264,] -13.10630388 19.8463306
[265,] 7.63777241 -1.3282032
[266,] -6.87501220 5.8439681
[267,] -4.72081621 -4.5070830
[268,] 3.15877535 -1.8554563
[269,] -2.48001313 -0.6650514
[270,] -2.10611109 1.1680888
[271,] -2.32732138 8.6563767
[272,] -8.02471762 -2.0008769
[273,] -24.17275654 24.3013553
[274,] 9.81492472 -4.5525786
[275,] -4.78429175 7.5213815
[276,] -1.27430904 11.8706420
[277,] -15.08763613 20.3938039
[278,] -0.86232169 6.4867035
[279,] 4.63142715 -1.6495709
[280,] -14.30939885 14.4674472
[281,] 0.80110719 8.7969383
[282,] -14.38556949 28.9016046
[283,] 5.94634421 -5.9838622
[284,] -8.44679097 12.9455645
[285,] 8.84851949 6.4262388
[286,] -31.09846274 32.1714756
[287,] 1.19518121 -8.4949273
[288,] -8.13636448 26.8071693
[289,] -17.46826062 23.9195228
[290,] -5.60339869 -5.5868645
[291,] 0.62041611 -2.8699140
[292,] -9.91683366 19.8964891
[293,] -3.16660031 14.6731365
[294,] 1.21309454 3.4129999
[295,] -16.49924627 20.0975155
[296,] -19.85914634 17.9128731
[297,] -0.28233836 15.1753103
[298,] -8.28401323 12.7044897
[299,] -6.02042904 4.5783254
[300,] -16.76376010 20.4892620
[301,] -17.70216601 33.8135036
[302,] -20.97824333 19.5702624
[303,] -3.71354131 3.5487025
[304,] -13.99132024 30.7046105
[305,] -4.89107083 12.4533048
[306,] -6.53919549 14.8941871
[307,] 3.70815023 -2.6690837
[308,] -15.85578741 16.7576577
[309,] -6.04581926 9.3897112
[310,] 11.99955392 -24.4962670
[311,] -8.46452908 20.1325089
[312,] -17.24948422 28.3692964
[313,] -8.25862302 7.8931039
[314,] -8.55861306 22.6587392
[315,] 3.43355041 7.2851658
[316,] 13.96575718 -10.6999859
[317,] 5.39192632 -0.3889833
[318,] -11.02584465 11.9913754
[319,] 8.34992503 -2.3829054
[320,] -16.39246719 15.1655923
[321,] -4.93680827 17.2948249
[322,] -9.64971071 26.6615526
[323,] 5.68183037 -5.5921156
[324,] -17.62338625 26.5361562
[325,] -5.32862363 3.5537575
[326,] 4.31334855 -17.8867343
[327,] -8.25097090 10.2686624
[328,] -13.41916426 17.9227872
[329,] -14.07270911 30.8251479
[330,] -8.47739942 3.4433302
[331,] -12.63831786 19.1532405
[332,] -13.01221990 17.3201002
[333,] -8.04749873 9.9673189
[334,] -24.74995552 41.8644300
[335,] -6.18824978 9.6006517
[336,] -3.42102815 5.5023801
[337,] 2.12871935 2.0569541
[338,] -13.24630052 8.1192095
[339,] -5.45574994 8.5158151
[340,] 1.62508190 -1.9709386
[341,] -0.78354193 -0.7906439
[342,] -13.28681972 27.2743497
[343,] -17.60060515 14.5679603
[344,] -12.85726949 -4.3914046
[345,] -13.13691232 10.3440963
[346,] -2.34766860 8.6865111
[347,] 3.56328582 9.4799182
[348,] 1.50056470 10.1479290
[349,] -9.27859302 2.2430113
[350,] -15.40814861 16.0947020
[351,] 10.64916066 -5.7880869
[352,] -9.11824916 13.9399980
[353,] -14.67808265 26.9479270
[354,] -2.03480822 10.6100544
[355,] -2.12889220 13.1362847
[356,] 10.94932593 -1.4588507
[357,] -18.64074715 28.0428737
[358,] -11.41748479 17.3451795
[359,] -7.46264763 -5.2201973
[360,] -10.21438982 22.7240629
[361,] -1.44734801 2.5793482
[362,] -24.74247864 25.1451171
[363,] -19.82088579 29.7906659
[364,] -14.84086040 27.1890017
[365,] -23.50129835 23.3069217
[366,] -19.24612069 24.1656527
[367,] -7.10387459 10.9566974
[368,] 4.80933389 -16.2344001
[369,] -0.22651493 0.7712872
[370,] -16.56533092 24.9691700
[371,] 8.10071542 2.7599583
[372,] 5.22410558 4.6333430
[373,] -24.84925773 30.0770403
[374,] 7.22578505 4.0557353
[375,] -10.91384734 21.3730723
[376,] -30.18283794 30.8154299
[377,] -15.35475907 13.6287404
[378,] -19.74210603 22.5133185
[379,] -9.16659571 11.6247082
[380,] -11.47348345 12.6543311
[381,] -35.60024090 43.6124184
[382,] 1.39100128 -11.1718293
[383,] -3.95248970 18.2239347
[384,] 6.76023292 -7.1892362
[385,] -20.85859390 31.3275178
[386,] -6.57484693 10.1732043
[387,] -0.02043364 7.6267537
[388,] -11.07662508 21.6141471
[389,] -24.55413545 39.1875280
[390,] 20.63721077 -8.6459911
[391,] 16.64637172 -28.9913401
[392,] -2.17723874 10.8209948
[393,] 20.58625511 -18.1180910
[394,] -13.15969342 22.3122922
[395,] -11.63887030 5.7385959
[396,] 3.55041549 -7.2092604
[397,] -1.10648830 6.8483157
[398,] -18.85952355 23.5931000
[399,] -1.33795981 4.8042350
[400,] -12.95883035 14.8541386
[401,] -15.87856851 28.7258536
[402,] -1.85672625 15.1200967
[403,] -29.80632679 39.8053802
[404,] -15.17163411 13.3575313
[405,] -3.61945733 1.0224721
[406,] -22.01838532 33.0451757
[407,] -14.04488501 14.0757006
[408,] 2.28627886 -12.4977407
[409,] 5.10967439 7.1897077
[410,] -19.91757888 25.1600862
[411,] 3.31651010 2.6847204
[412,] -26.53807682 32.5781913
[413,] -10.61124818 13.7642470
[414,] -0.66650162 3.8098015
[415,] -11.75069239 15.4517706
[416,] -15.42327761 30.4384564
[417,] 2.86121919 0.9721175
[418,] -13.04526222 19.7559275
[419,] -13.58194200 18.1638620
[420,] -14.22296698 9.5656583
[421,] -6.39433108 2.7451851
[422,] -5.54740003 -0.8960161
[423,] -7.68124880 9.4249006
[424,] -1.69151462 2.9409604
[425,] -6.43745940 14.7435153
[426,] -12.69431652 14.4623921
[427,] -31.48245077 39.9008383
[428,] -2.91234770 4.7490214
[429,] -5.23958265 5.8087787
[430,] -5.53713881 8.6363525
[431,] 5.31575568 14.0451742
[432,] -6.11694691 19.0426172
[433,] -29.98945175 40.0765893
[434,] -4.92411316 14.8891320
[435,] -8.14419182 5.3367392
[436,] -13.96610526 6.7983532
[437,] -14.90694505 32.0606563
[438,] -3.27094551 7.6669982
[439,] 4.92133120 -6.8527032
[440,] -7.11917881 6.2055803
[441,] 8.85860548 -3.1362641
[442,] -2.88434837 7.0944456
[443,] -6.19068367 21.5387132
[444,] 9.71057952 -11.5587169
[445,] 0.37885861 4.6485082
[446,] -10.46377466 8.7720551
[447,] -7.44212519 13.8445399
[448,] -24.18545165 26.7070482
[449,] -27.71578157 22.3879221
[450,] 2.42123251 4.0106318
[451,] 0.80875930 11.1724969
[452,] 9.36467682 -11.0464329
[453,] 6.47537187 -6.7673553
[454,] 3.52502527 -2.3978746
[455,] -16.38742419 10.3843408
[456,] -3.40329004 -1.6845643
[457,] -18.04563483 22.3877261
[458,] -11.34374803 14.8490836
[459,] -18.20580346 29.7856109
[460,] -12.13972341 27.9623847
[461,] -0.50615776 15.5067882
[462,] -4.17387521 6.6173511
[463,] 9.35198171 -8.6407400
[464,] -13.01221990 17.3201002
[465,] -4.53247302 9.5353279
[466,] -6.24668233 16.8478647
[467,] -2.51044634 8.9275858
[468,] -23.27486984 30.1322539
[469,] -10.81211125 21.2224005
[470,] -9.25807058 21.3077485
[471,] -1.56438832 -2.0210972
[472,] -1.92037702 8.0536897
[473,] 3.54032949 2.3532426
[474,] -10.37716756 22.9651377
[475,] -5.52444370 6.2306596
[476,] -9.35980667 21.4584202
[477,] 16.84236701 -12.5733707
[478,] -12.25432984 11.4238778
[479,] -6.73779990 -8.6805924
[480,] -4.53751602 14.3165794
[481,] -17.11731492 18.6259874
[482,] -5.49905349 1.4192738
[483,] -3.21494686 12.3578466
[484,] -1.54665022 -9.2080416
[485,] 0.69676198 1.7908000
[486,] 20.05983656 -10.1777879
[487,] -10.45107955 6.3663622
[488,] -6.32563731 5.0303406
[489,] -13.51829123 25.2302690
[490,] -9.88379134 17.4606619
[491,] -11.67191263 8.1744231
[492,] -10.55524953 18.4550954
[493,] -1.02770854 -0.4290317
[494,] -12.19328818 11.3334748
[495,] 12.70422967 -8.8316562
[496,] 15.77161658 -8.6006916
[497,] -21.71074317 20.6550990
[498,] -2.75965595 14.0704495
[499,] -18.63309504 30.4184322
[500,] -2.91739070 9.5302728
[ reached getOption("max.print") -- omitted 500 rows ]The object returned is a list. The element names are $optimalTx and $decisionFunc and correspond to \(\widehat{d}^{opt}_{Q,1}(H_{1i})\) and \(Q(H_{1i},a_{1};\widehat{\beta}_{1})\), respectively.
Function DynTxRegime::
DynTxRegime::estimator(x = result)[1] 13.21562Function DynTxRegime::
The first new patient has the following baseline covariates
print(x = patient1) SBP0 W K Cr Ch
1 162 72.6 4.2 0.8 209.2The recommended treatment based on the previous analysis is obtained by providing the object returned by DynTxRegime::
DynTxRegime::optTx(x = result, newdata = patient1)$optimalTx
[1] 1
$decisionFunc
0 1
[1,] -6.574847 10.1732Treatment A= 1 is recommended as \(Q_{1}(H_{1i},1;\widehat{\beta}_{1})\) is larger than \(Q_{1}(H_{1i},0;\widehat{\beta}_{1})\)
The second new patient has the following baseline covariates
print(x = patient2) SBP0 W K Cr Ch
1 153 68.2 4.5 0.8 178.8And the recommended treatment is obtained by calling
DynTxRegime::optTx(x = result, newdata = patient2)$optimalTx
[1] 0
$decisionFunc
0 1
[1,] 3.296163 2.714855Treatment A= 0 is recommended as \(Q_{1}(H_{1i},0;\widehat{\beta}_{1})\) is larger than \(Q_{1}(H_{1i},1;\widehat{\beta}_{1})\)
Value Search Estimators
For binary treatment \(A_{1}\) coded as {0,1}, the augmented inverse probability weighted estimator for the value of regime \(d_{1}(H_{1}; \eta_{1})\) with fixed \(\eta = \eta_{1}\) is
\[ \widehat{\mathcal{V}}_{AIPW}(d_{\eta}) = n^{-1} \sum_{i=1}^{n} \left[ \frac{\mathcal{C}_{d_{\eta},i} Y_{i}}{\pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})} - \frac{\mathcal{C}_{d_{\eta},i} - \pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})}{\pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})} \mathcal{Q}_{d_{\eta},1} (H_{1i}; \eta_{1}, \widehat{\beta}_{1}) \right], \]
where \(C_{d_{\eta}} = \text{I}\{A_{1} = d_{1}(H_{1}; \eta_{1})\}\) is the indicator of whether or not the treatment option actually received coincides with the option dictated by \(d\). The propensity for receiving treatment consistent with regime \(d\) given an individual’s history is \(\pi_{d,1}(H_{1}) = P(\mathcal{C}_{d} = 1|H_{1})\). It is straightforward to deduce that,
\[ \pi_{d,1}(H_{1}) = \pi_{1}(H_{1}) ~ \text{I}\{d_{1}(H_{1}) = 1\} + \{1-\pi_{1}(H_{1})\} ~ \text{I}\{d_{1}(H_{1}) = 0\}, \] which can be estimated by positing a model \(\pi_{1}(H_{1};\gamma_{1})\) for \(\pi_{1}(H_{1}) = P(A_{1} = 1|H_{1})\). Thus
\[ \pi_{d,1}(H_{1}; \gamma_{1}) = \pi_{1}(H_{1}; \gamma_{1}) ~ \text{I}\{d_{1}(H_{1}) = 1\} + \{1-\pi_{1}(H_{1}; \gamma_{1})\} ~ \text{I}\{d_{1}(H_{1}) = 0\}, \] and \(\widehat{\gamma}_{1}\) is a suitable estimator for \(\gamma_{1}\).
Finally, \[ \mathcal{Q}_{d_{\eta},1} (H_{1}; \eta_{1}, \beta_{1})= \sum_{a_{1} \in \mathcal{A}_{1}} Q_{1}(H_{1},a_{1} ; \beta_{1})~\text{I}\{d_{1}(H_{1}; \eta_{1})=a_{1}\}, \]
where \(Q_{1}(h_{1},a_{1}; \beta_{1})\) is a model for \(Q_{1}(h_{1},a_{1})=E(Y | H_{1}=h_{1},A_{1}=a_{1})\) and \(\widehat{\beta}_{1}\) is a suitable estimator for \(\beta_{1}\).
The optimal treatment regime, \(\widehat{d}_{\eta,AIPW}^{opt} = \{d_{1}(h_{1},\widehat{\eta}_{1,AIPW}^{opt})\}\), is that which maximizes the value, and thus
\[ \widehat{\eta}_{1,AIPW}^{opt} = \underset{\eta_{1}}{\mathrm{\arg\!\max}}~n^{-1} \sum_{i=1}^{n} \left[\frac{\mathcal{C}_{d_{\eta},i} Y_{i}}{\pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})} - \frac{\mathcal{C}_{d_{\eta},i} - \pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})}{\pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})} \mathcal{Q}_{d_{\eta},1} (H_{1i}; \eta_{1}, \widehat{\beta}_{1}) \right]. \]
The simple inverse probability weighted estimator is the special case where \(\mathcal{Q}_{d_{\eta},1}(h_{1},a_{1}) \equiv 0\):
\[ \widehat{\mathcal{V}}_{IPW}(d_{\eta}) = n^{-1} \sum_{i=1}^{n} \frac{\mathcal{C}_{d_{\eta},i} Y_{i}}{\pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})}, \]
and the optimal treatment regime is \(\widehat{d}_{\eta,IPW}^{opt} = \{d_{1}(h_{1},\widehat{\eta}_{1,IPW}^{opt})\}\) is defined in terms of \(\widehat{\eta}_{1,IPW}^{opt}\)
\[ \widehat{\eta}_{1,IPW}^{opt} = \underset{\eta_{1}}{\mathrm{\arg\!\max}}~n^{-1} \sum_{i=1}^{n} \frac{\mathcal{C}_{d_{\eta},i} Y_{i}}{\pi_{d_{\eta,1}}(H_{1i}; \eta_{1}, \widehat{\gamma}_{1})} . \]
A general implementation of the value search estimator is provided in
utils::str(object = DynTxRegime::optimalSeq)function (..., moPropen, moMain, moCont, data, response, txName, regimes, fSet = NULL, refit = FALSE, iter = 0L, verbose = TRUE) We briefly describe the input arguments for DynTxRegime::
| Input Argument | Description |
|---|---|
| \(\dots\) | Additional inputs to be provided to genetic algorithm. |
| moPropen | A “modelObj” object. The modeling object for the propensity score regression step. |
| moMain | A “modelObj” object. The modeling object for the \(\nu_{1}(h_{1}; \phi_{1})\) component of \(Q_{1}(h_{1},a_{1};\beta_{1})\). |
| moCont | A “modelObj” object. The modeling object for the \(\text{C}_{1}(h_{1}; \psi_{1})\) component of \(Q_{1}(h_{1},a_{1};\beta_{1})\). |
| data | A “data.frame” object. The covariate history and the treatment received. |
| response | A “numeric” vector. The outcome of interest, where larger values are better. |
| txName | A “character” object. The column header of data corresponding to the treatment variable. |
| regimes | A “function”. A user defined function specifying the class of treatment regime under consideration. |
| fSet | A “function”. A user defined function specifying treatment or model subset structure. |
| refit | Deprecated. |
| iter | An “integer” object. The maximum number of iterations for iterative algorithm. |
| verbose | A “logical” object. If TRUE progress information is printed to screen. |
Methods implemented in DynTxRegime break the outcome model into two components: a main effects component and a contrasts component. For example, for binary treatments, \(Q_{1}(h_{1}, a_{1}; \beta_{1})\) can be written as
\[ Q_{1}(h_{1}, a_{1}; \beta_{1})= \nu_{1}(h_{1}; \phi_{1}) + a_{1} \text{C}_{1}(h_{1}; \psi_{1}), \]
where \(\beta_{1} = (\phi^{\intercal}_{1}, \psi^{\intercal}_{1})^{\intercal}\). Here, \(\nu_{1}(h_{1}; \phi_{1})\) comprises the terms of the outcome regression model that are independent of treatment (so called “main effects” or “common effects”), and \(\text{C}_{1}(h_{1}; \psi_{1})\) comprises the terms of the model that interact with treatment (so called “contrasts”). Input arguments moMain and moCont specify \(\nu_{1}(h_{1}; \phi_{1})\) and \(\text{C}_{1}(h_{1}; \psi_{1})\), respectively.
In the examples provided in this chapter, the two components of \(Q_{1}(h_{1}, a_{1}; \beta_{1})\) are both linear models, the parameters of which are estimated using stats::
DynTxRegime::
The value object returned by DynTxRegime::
| Slot Name | Description |
|---|---|
| @analysis@genetic | The genetic algorithm results. |
| @analysis@propen | The propensity regression analysis. |
| @analysis@outcome | The outcome regression analysis. NA if IPW. |
| @analysis@regime | The \(\widehat{d}^{opt}_{\eta}\) definition. |
| @analysis@call | The unevaluated function call. |
| @analysis@optimal | The estimated value and optimal treatment for the training data. |
There are several methods available for objects of this class that assist with model diagnostics, the exploration of training set results, and the estimation of optimal treatments for future patients. We explore methods under the Methods tab.
We continue to consider the three propensity score models and the three outcome regression models introduced in Chapter 2, which represent a range of model (mis)specification. For brevity, we illustrate the call to DynTxRegime::
The inverse probability weighted value estimator does not have an outcome regression step, and thus moMain and moCont are not provided as input or are set to NULL. Further iter is kept at its default value of 0.
Input moPropen is a modeling object for the propensity score regression. To illustrate the function call for the inverse probability weighted method, we will use the true propensity score model
\[ \pi^{3}_{1}(h_{1};\gamma_{1}) = \frac{\exp(\gamma_{10} + \gamma_{11}~\text{SBP0} + \gamma_{12}~\text{Ch})}{1+\exp(\gamma_{10} + \gamma_{11}~\text{SBP0}+ \gamma_{12}~\text{Ch})}, \] which is defined as a modeling object as follows
p3 <- modelObj::buildModelObj(model = ~ SBP0 + Ch,
solver.method = 'glm',
solver.args = list(family='binomial'),
predict.method = 'predict.glm',
predict.args = list(type='response'))As for all methods discussed in this chapter: the “data.frame” containing the baseline covariates and treatment received is data set dataSBP, the treatment is contained in column $A of dataSBP, and the outcome of interest is the change in systolic blood pressure measured six months after treatment, \(y = \text{SBP0} - \text{SBP6}\), which is already defined in our R environment.
To allow for direct comparison with the outcome regression estimator, the restricted class of regimes that we will consider is characterized by rules of the form
\[ d_{1}(h_{1};\eta_{1}) = \text{I}(\eta_{11} + \eta_{12}~\text{Ch} + \eta_{13} ~ \text{K} > 0). \]
The rule is specified using a user-defined function, which is passed to the method through input regimes. The user-defined function must accept as input the regime parameter names and the data set, and the function must return a vector of the recommended treatment. For this regime, the function can be specified as
reg <- function(eta11, eta12, eta13, data) {
tmp <- eta11 + eta12 * data$Ch + eta13 * data$K > 0.0
return( as.integer(x = tmp) )
}where inputs eta11, eta12, and eta13 are the parameters of the regime to be estimated and data is the a ‘data.frame’ object for the analysis. This structure for the input argument list (all parameter names followed by data) is required. Note that the function
- defines the regime for the entire data set, and
- returns values of the same class as the treatment variable.
Circumstances under which this input would be utilized are not represented by the data set generated for illustration in this chapter.
- the search space for the \(\eta\) parameters,
- initial guess for the \(\eta\) parameters, and
- population size for the algorithm.
Because rgenoud::
Domains <- rbind( c(-1.0,1.0), c(-1.0,1.0), c(-1.0,1.0) )
starting.values <- c(0.0, 0.0, 0.0)
pop.size <- 1000LFor additional information on these and other available inputs for the genetic algorithm, please see ?rgenound::genoud.
The optimal treatment regime, \(\widehat{d}_{\eta, IPW}^{opt}(h_{1})\), is estimated as follows.
IPW3 <- DynTxRegime::optimalSeq(moPropen = p3,
data = dataSBP,
response = y,
txName = 'A',
regimes = reg,
Domains = Domains,
pop.size = pop.size,
starting.values = starting.values,
verbose = TRUE)IPW estimator will be used
Value Search - Missing Data Perspective.
Propensity for treatment regression.
Regression analysis for moPropen:
Call: glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Coefficients:
(Intercept) SBP0 Ch
-15.94153 0.07669 0.01589
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 1378
Residual Deviance: 1162 AIC: 1168
Outcome regression.
No outcome regression performed.
Genetic Algorithm
$value
[1] 13.09007
$par
[1] -0.38167184 0.02356612 -0.87251940
$gradients
[1] NA NA NA
$generations
[1] 14
$peakgeneration
[1] 3
$popsize
[1] 1000
$operators
[1] 122 125 125 125 125 126 125 126 0
Recommended Treatments:
0 1
216 784
Estimated value: 13.09007 Above, we opted to set verbose to TRUE to highlight some of the information that should be verified by a user. Notice the following:
- The first line of the verbose output indicates that the selected value estimator is the inverse probability weighted estimator and that the estimator is from the missing data perspective.
Users should verify that this is the intended estimator. - The information provided for the propensity regression is not defined within DynTxRegime::
optimalSeq() , but is specified by the statistical method selected to obtain parameter estimates; in this example it is defined by stats::glm() .
Users should verify that the model was correctly interpreted by the software and that there are no warnings or messages reported by the regression method. - A statement indicates that no outcome regression was performed.
If the augmented inverse probability weighted estimator is desired, this should not be the case. - The results of the genetic algorithm used to optimize over \(\eta_{1}\) show the estimated value \(\widehat{\mathcal{V}}_{IPW}(d_{\eta})\) and the estimated parameters of the optimal restricted regime.
Users should verify that the regime was correctly interpreted by the software and that there are no warnings or messages reported by rgenoud::genoud() . - Finally, a tabled summary of the recommended treatments and the estimated value for the training data are shown. The sum of the elements of the table should be the number of individuals in the training data. If it is not, the data set is likely not complete; method implementation in DynTxRegime require complete data sets.
The first step of the post-analysis should always be model diagnostics. DynTxRegime comes with several tools to assist in this task. However, we have explored the outcome regression models previously and will skip that step here. Available model diagnostic tools are described under the Methods tab.
The first step of the post-analysis should always be model diagnostics. DynTxRegime comes with several tools to assist in this task. However, we have explored the propensity score model previously and will skip that step here. Many of the model diagnostic tools are described under the Methods tab.
The estimated parameters of the optimal treatment regime can be retrieved using DynTxRegime::
DynTxRegime::regimeCoef(object = IPW3) eta11 eta12 eta13
-0.38167184 0.02356612 -0.87251940 To determine the parameters uniquely, we further require that \(|n_{1}| = 1\). From this, the estimated optimal treatment regime is
\[ d_{1}(h_{1};\widehat{\eta}_{1}) = \text{I} (-0.40 + 0.02 Ch - 0.92 K > 0). \]
There are several methods available for the returned object that assist with model diagnostics, the exploration of training set results, and the estimation of optimal treatments for future patients. A complete description of these methods can be found under the Methods tab.
For the augmented inverse probability weighted value estimator, moMain and moCont are modeling objects specifying the outcome regression. To illustrate, we will use the true outcome regression model
\[ Q^{3}_{1}(h_{1},a_{1};\beta_{1}) = \beta_{10} + \beta_{11} \text{Ch} + \beta_{12} \text{K} + a_{1}~(\beta_{13} + \beta_{14} \text{Ch} + \beta_{15} \text{K}), \]
which is defined as modeling objects as follows
q3Main <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')q3Cont <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')Note that the formula in the contrast component does not contain the treatment variable; it contains only the covariates that interact with the treatment.
Both components of the outcome regression model are of the same class, and the models for each decision point should be fit as a single combined object. Thus, the iterative algorithm is not required, and iter should keep its default value.
Input moPropen is a modeling object for the propensity score regression. We will again use the true propensity score model
\[ \pi^{3}_{1}(h_{1};\gamma_{1}) = \frac{\exp(\gamma_{10} + \gamma_{11}~\text{SBP0} + \gamma_{12}~\text{Ch})}{1+\exp(\gamma_{10} + \gamma_{11}~\text{SBP0}+ \gamma_{12}~\text{Ch})}, \] which is defined as a modeling object as follows
p3 <- modelObj::buildModelObj(model = ~ SBP0 + Ch,
solver.method = 'glm',
solver.args = list(family='binomial'),
predict.method = 'predict.glm',
predict.args = list(type='response'))As for all methods discussed in this chapter: the “data.frame” containing the baseline covariates and treatment received is data set dataSBP, the treatment is contained in column $A of dataSBP, and the outcome of interest is the change in systolic blood pressure measured six months after treatment, \(y = \text{SBP0} - \text{SBP6}\), which is already defined in our R environment.
To allow for direct comparison with the outcome regression estimator, the restricted class of regimes that we will consider is characterized by rules of the form
\[ d_{1}(h_{1};\eta_{1}) = \text{I}(\eta_{11} + \eta_{12}~\text{Ch} + \eta_{13} ~ \text{K} > 0). \]
The rule is specified using a user-defined function, which is passed to the method through input regimes. The user-defined function must accept as input the regime parameter names and the data set, and the function must return a vector of the recommended treatment. For this regime, the function can be specified as
reg <- function(eta11, eta12, eta13, data) {
tmp <- eta11 + eta12 * data$Ch + eta13 * data$K > 0.0
return( as.integer(x = tmp) )
}where inputs eta11, eta12, and eta13 are the parameters of the regime to be estimated and data is the a ‘data.frame’ object for the analysis. This structure for the input argument list (all parameter names followed by data) is required. Note that the function
- defines the regime for the entire data set, and
- returns values of the same class as the treatment variable.
Circumstances under which this input would be utilized are not represented by the data set generated for illustration in this chapter.
- the search space for the \(\eta\) parameters,
- initial guess for the \(\eta\) parameters, and
- population size for the algorithm.
Because rgenoud::
Domains <- rbind( c(-1.0,1.0), c(-1.0,1.0), c(-1.0,1.0) )
starting.values <- c(0.0, 0.0, 0.0)
pop.size <- 1000LFor additional information on these and other available inputs for the genetic algorithm, please see ?rgenound::genoud.
The optimal treatment regime, \(\widehat{d}_{AIPW,1}^{opt}(h_{1})\), is estimated as follows.
AIPW33 <- DynTxRegime::optimalSeq(moPropen = p3,
moMain = q3Main,
moCont = q3Cont,
data = dataSBP,
response = y,
txName = 'A',
regimes = reg,
Domains = Domains,
pop.size = pop.size,
starting.values = starting.values,
verbose = TRUE)Value Search - Missing Data Perspective.
Propensity for treatment regression.
Regression analysis for moPropen:
Call: glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Coefficients:
(Intercept) SBP0 Ch
-15.94153 0.07669 0.01589
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 1378
Residual Deviance: 1162 AIC: 1168
Outcome regression.
Combined outcome regression model: ~ Ch+K + A + A:(Ch+K) .
Regression analysis for Combined:
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) Ch K A Ch:A K:A
-15.6048 -0.2035 12.2849 -61.0979 0.5048 -6.6099
Genetic Algorithm
$value
[1] 13.14356
$par
[1] -0.92419308 0.01204358 -0.27660824
$gradients
[1] NA NA NA
$generations
[1] 19
$peakgeneration
[1] 8
$popsize
[1] 1000
$operators
[1] 122 125 125 125 125 126 125 126 0
Recommended Treatments:
0 1
221 779
Estimated value: 13.14356 Above, we opted to set verbose to TRUE to highlight some of the information that should be verified by a user. Notice the following:
- The first line of the verbose output indicates that the selected value estimator is the value search estimator from the missing data perspective.
Users should verify that this is the intended estimator. - The information provided for the propensity score and outcome regressions is not defined within DynTxRegime::
optimalSeq() , but is specified by the statistical method selected to obtain parameter estimates; in this example it is defined by stats::glm() and stats::lm() .
Users should verify that the models were correctly interpreted by the software and that there are no warnings or messages reported by the regression methods. - The results of the genetic algorithm used to optimize over \(\eta_{1}\) show the estimated value, \(\widehat{\mathcal{V}}_{AIPW}(d_{\eta})\), and the estimated parameters of the optimal restricted regime.
Users should verify that the model was correctly interpreted by the software and that there are no warnings or messages reported by rgenoud::genoud() . - Finally, a tabled summary of the recommended treatments and the estimated value for the training data are shown. The sum of the elements of the table should be the number of individuals in the training data. If it is not, the data set is likely not complete; method implementation in DynTxRegime require complete data sets.
The first step of the post-analysis should always be model diagnostics. DynTxRegime comes with several tools to assist in this task. However, we have explored the outcome regression models previously and will skip that step here. Available model diagnostic tools are described under the Methods tab.
The estimated parameters of the optimal treatment regime can be retrieved using DynTxRegime::
DynTxRegime::regimeCoef(object = AIPW33) eta11 eta12 eta13
-0.92419308 0.01204358 -0.27660824 To determine the parameters uniquely, we further require that \(|n_{1}| = 1\). From this, the estimated optimal treatment regime is
\[ d_{1}(h_{1};\widehat{\eta}_{1}) = \text{I} (-0.96 + 0.01 Ch - 0.29 K > 0). \]
There are several methods available for the returned object that assist with model diagnostics, the exploration of training set results, and the estimation of optimal treatments for future patients. A complete description of these methods can be found under the Methods tab.
In the table below, we show the estimated value obtained using the simple inverse probability weighted estimator under each of the propensity score models considered and using the augmented inverse probability weighted estimator under all combinations of the outcome and propensity score models. In parentheses, we show the total number of individuals in the training data recommended to each treatment. The shaded region indicates the results for the augmented inverse probability weighted estimator.
| (mmHg) | \(\widehat{\mathcal{V}}_{IPW}(d^{opt})\) | \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) |
| \(\pi^{1}_{1}(h_{1};\gamma_{1})\) | 16.95 (216, 784) | 16.05 (188, 812) | 13.26 (219, 781) | 13.13 (219, 781) |
| \(\pi^{2}_{1}(h_{1};\gamma_{1})\) | 13.23 (217, 783) | 13.21 (261, 739) | 13.20 (217, 783) | 13.13 (219, 781) |
| \(\pi^{3}_{1}(h_{1};\gamma_{1})\) | 13.09 (216, 784) | 13.19 (243, 757) | 13.19 (217, 783) | 13.14 (221, 779) |
Next, we show the parameters of the estimated optimal treatment regime obtained using the same estimators and model combinations as above.
| (\(\widehat{\eta}_{1},\widehat{\eta}_{2},\widehat{\eta}_{3}\)) | IPW | \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) |
| \(\pi^{1}_{1}(h_{1};\gamma_{1})\) | (-0.40, 0.02, -0.92) | (-0.80, 0.02, -0.60) | (-0.97, 0.01, -0.23) | (-0.97, 0.01, -0.23) |
| \(\pi^{2}_{1}(h_{1};\gamma_{1})\) | (-0.98, 0.01, -0.19) | (-0.79, 0.02, -0.62) | (-0.98, 0.01, -0.21) | (-0.97, 0.01, -0.22) |
| \(\pi^{3}_{1}(h_{1};\gamma_{1})\) | (-0.40, 0.02, -0.92) | (-0.83, 0.02, -0.55) | (-0.97, 0.01, -0.22) | (-0.96, 0.01, -0.29) |
We illustrate the methods available for objects of class “OptimalSeqMissing” by considering the following analysis:
q3Main <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')q3Cont <- modelObj::buildModelObj(model = ~ (Ch + K),
solver.method = 'lm',
predict.method = 'predict.lm')p3 <- modelObj::buildModelObj(model = ~ SBP0 + Ch,
solver.method = 'glm',
solver.args = list(family='binomial'),
predict.method = 'predict.glm',
predict.args = list(type='response'))reg <- function(eta11, eta12, eta13, data) {
tmp <- eta11 + eta12 * data$Ch + eta13 * data$K > 0.0
return( as.integer(x = tmp) )
}Domains <- rbind( c(-1.0,1.0), c(-1.0,1.0), c(-1.0,1.0) )
starting.values <- c(0.0, 0.0, 0.0)
pop.size <- 1000Lresult <- DynTxRegime::optimalSeq(moPropen = p3,
moMain = q3Main,
moCont = q3Cont,
data = dataSBP,
response = y,
txName = 'A',
regimes = reg,
Domains = Domains,
pop.size = pop.size,
starting.values = starting.values,
verbose = FALSE)| Function | Description |
|---|---|
| Call(name, …) | Retrieve the unevaluated call to the statistical method. |
| coef(object, …) | Retrieve estimated parameters of postulated propensity and/or outcome models. |
| DTRstep(object) | Print description of method used to estimate the treatment regime and value. |
| estimator(x, …) | Retrieve the estimated value of the estimated optimal treatment regime for the training data set. |
| fitObject(object, …) | Retrieve the regression analysis object(s) without the modelObj framework. |
| genetic(object, …) | Retrieve the results of the genetic algorithm. |
| optTx(x, …) | Retrieve the estimated optimal treatment regime and decision functions for the training data. |
| optTx(x, newdata, …) | Predict the optimal treatment regime for new patient(s). |
| outcome(object, …) | Retrieve the regression analysis for the outcome regression step. |
| plot(x, suppress = FALSE, …) | Generate diagnostic plots for the regression object (input suppress = TRUE suppresses title changes indicating regression step.). |
| print(x, …) | Print main results. |
| propen(object, …) | Retrieve the regression analysis for the propensity score regression step |
| regimeCoef(object, …) | Retrieve the estimated parameters of the optimal restricted treatment regime. |
| show(object) | Show main results. |
| summary(object, …) | Retrieve summary information from regression analyses. |
The unevaluated call to the statistical method can be retrieved as follows
DynTxRegime::Call(name = result)DynTxRegime::optimalSeq(Domains = Domains, pop.size = pop.size,
starting.values = starting.values, int.seed = 1234L, unif.seed = 1234L,
moPropen = p3, moMain = q3Main, moCont = q3Cont, data = dataSBP,
response = y, txName = "A", regimes = reg, verbose = FALSE)The returned object can be used to re-call the analysis with modified inputs.
For example, to complete the analysis with a different outcome regression model requires only the following code.
q3Main <- modelObj::buildModelObj(model = ~ (K + Ch + Cr),
solver.method = 'lm',
predict.method = 'predict.lm')
eval(expr = DynTxRegime::Call(name = result))Value Search - Missing Data Perspective
Propensity Regression Analysis
moPropen
Call: glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Coefficients:
(Intercept) SBP0 Ch
-15.94153 0.07669 0.01589
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 1378
Residual Deviance: 1162 AIC: 1168
Outcome Regression Analysis
Combined
Call:
lm(formula = YinternalY ~ K + Ch + Cr + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) K Ch Cr A Ch:A K:A
-15.4733 12.2874 -0.2035 -0.1761 -61.0865 0.5048 -6.6132
Genetic
$value
[1] 13.14306
$par
[1] -0.92419308 0.01204358 -0.27660824
$gradients
[1] NA NA NA
$generations
[1] 19
$peakgeneration
[1] 8
$popsize
[1] 1000
$operators
[1] 122 125 125 125 125 126 125 126 0
Regime
eta11 eta12 eta13
-0.92419308 0.01204358 -0.27660824
Recommended Treatments:
0 1
221 779
Estimated value: 13.14306 This function provides a reminder of the analysis used to obtain the object.
DynTxRegime::DTRstep(object = result)Value Search - Missing Data PerspectiveThe
DynTxRegime::summary(object = result)$propensity
Call:
glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3891 -0.9502 -0.4940 0.9939 2.1427
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -15.941527 1.299952 -12.263 <2e-16 ***
SBP0 0.076687 0.007196 10.657 <2e-16 ***
Ch 0.015892 0.001753 9.066 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1377.8 on 999 degrees of freedom
Residual deviance: 1161.6 on 997 degrees of freedom
AIC: 1167.6
Number of Fisher Scoring iterations: 3
$outcome
$outcome$Combined
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Residuals:
Min 1Q Median 3Q Max
-9.0371 -1.9376 0.0051 2.0127 9.6452
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -15.604845 1.636349 -9.536 <2e-16 ***
Ch -0.203472 0.002987 -68.116 <2e-16 ***
K 12.284852 0.358393 34.278 <2e-16 ***
A -61.097909 2.456637 -24.871 <2e-16 ***
Ch:A 0.504816 0.004422 114.168 <2e-16 ***
K:A -6.609876 0.538386 -12.277 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.925 on 994 degrees of freedom
Multiple R-squared: 0.961, Adjusted R-squared: 0.9608
F-statistic: 4897 on 5 and 994 DF, p-value: < 2.2e-16
$genetic
$genetic$value
[1] 13.14356
$genetic$par
[1] -0.92419308 0.01204358 -0.27660824
$genetic$gradients
[1] NA NA NA
$genetic$generations
[1] 19
$genetic$peakgeneration
[1] 8
$genetic$popsize
[1] 1000
$genetic$operators
[1] 122 125 125 125 125 126 125 126 0
$regime
eta11 eta12 eta13
-0.92419308 0.01204358 -0.27660824
$optTx
0 1
221 779
$value
[1] 13.14356Though the required regression analyses are performed within the function, users should perform diagnostics to ensure that the posited models are suitable. DynTxRegime includes limited functionality for such tasks.
For most R regression methods, the following functions are defined.
The estimated parameters of the regression model(s) can be retrieved using DynTxRegime::
DynTxRegime::coef(object = result)$propensity
(Intercept) SBP0 Ch
-15.94152713 0.07668662 0.01589158
$outcome
$outcome$Combined
(Intercept) Ch K A Ch:A K:A
-15.6048448 -0.2034722 12.2848519 -61.0979087 0.5048157 -6.6098761 If defined by the regression methods, standard diagnostic plots can be generated using DynTxRegime::
graphics::par(mfrow = c(2,2))
DynTxRegime::plot(x = result)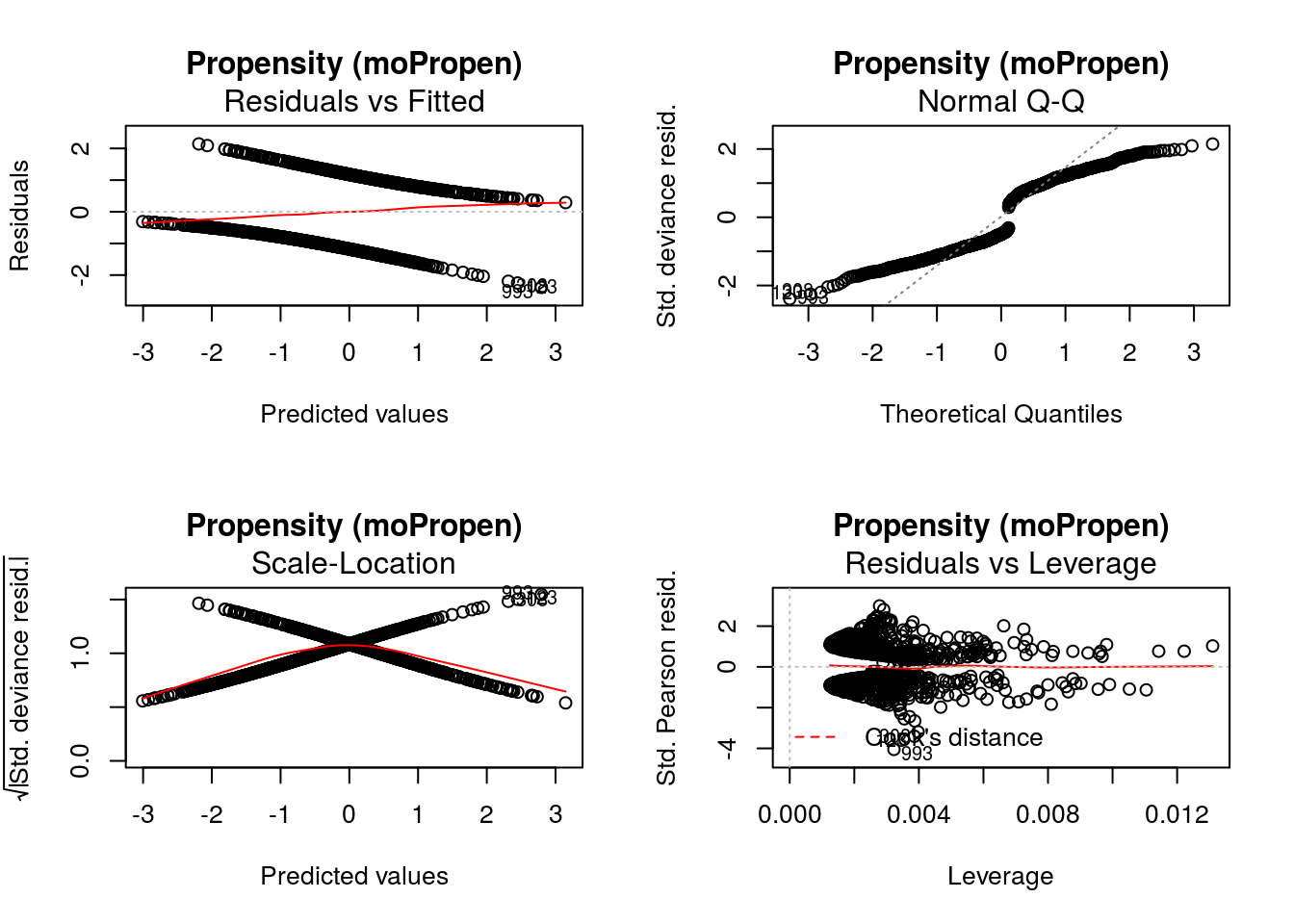
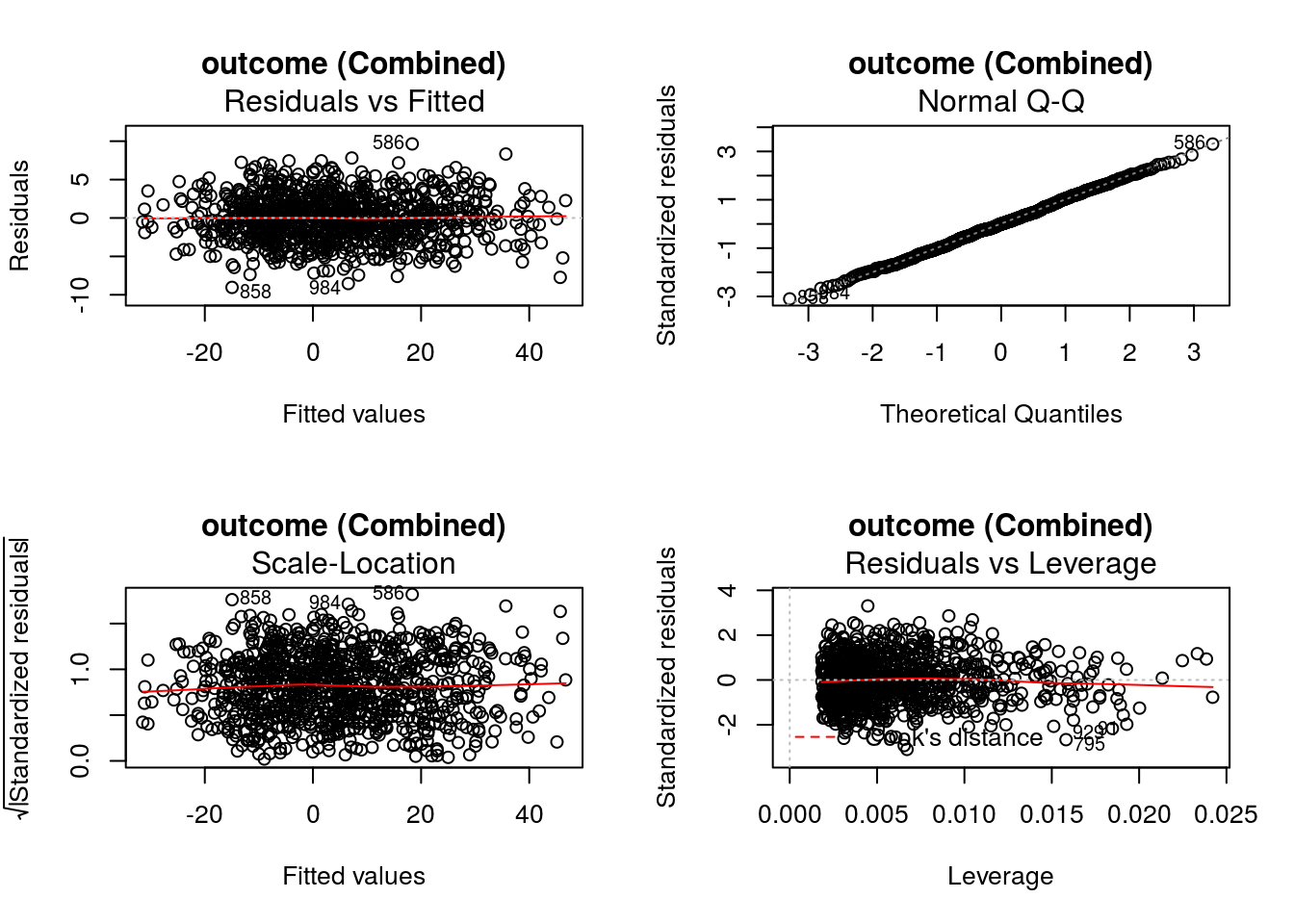
The value of input variable suppress determines if the plot titles are concatenated with an identifier of the regression analysis being plotted. For example, below we plot the Residuals vs Fitted for the propensity score and outcome regressions with and without the title concatenation.
graphics::par(mfrow = c(2,2))
DynTxRegime::plot(x = result, which = 1)
DynTxRegime::plot(x = result, suppress = TRUE, which = 1)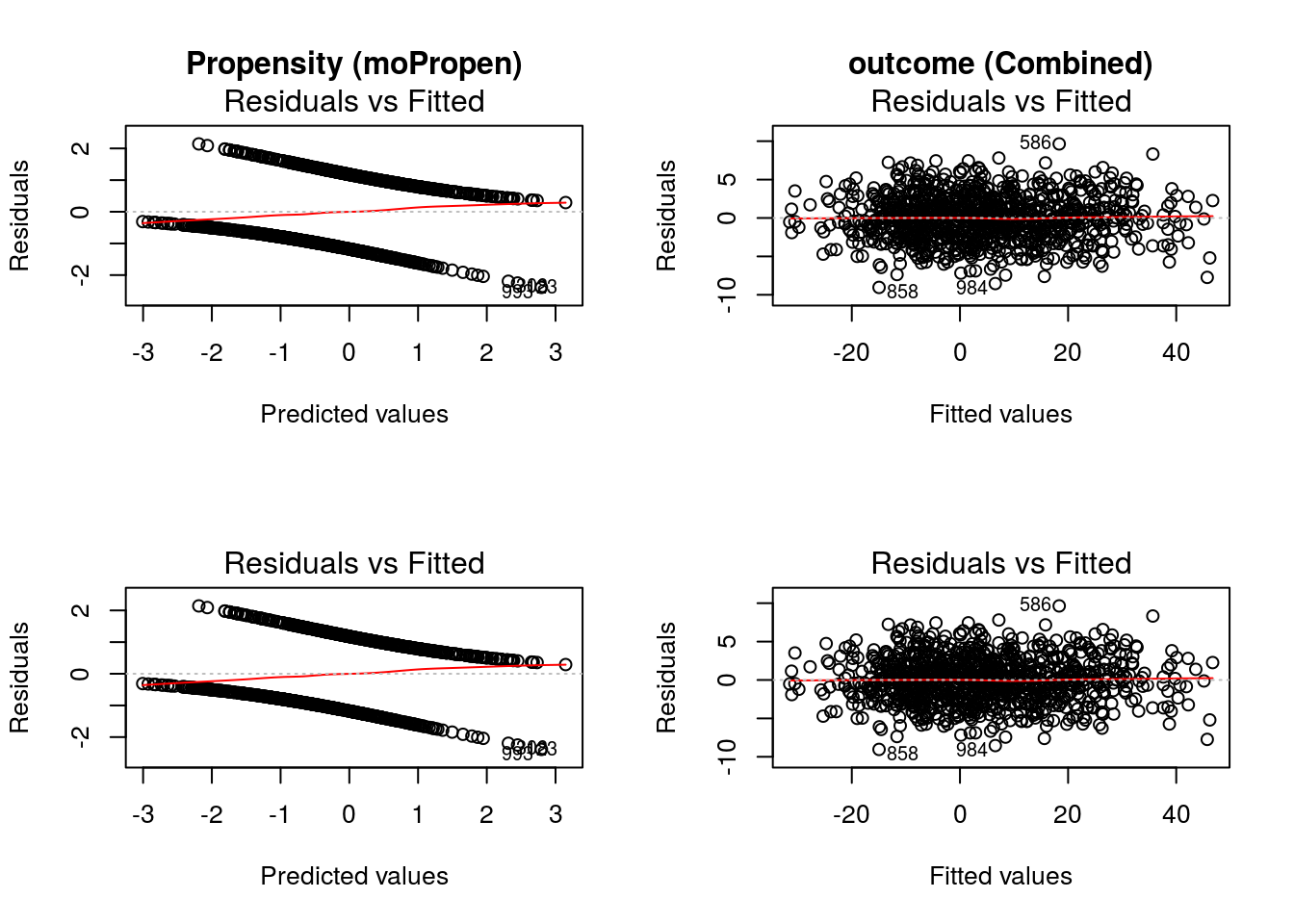
If there are additional diagnostic tools defined for a regression method used in the analysis but not implemented in DynTxRegime, the value object returned by the regression method can be extracted using function DynTxRegime::
fitObj <- DynTxRegime::fitObject(object = result)
fitObj$propensity
Call: glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Coefficients:
(Intercept) SBP0 Ch
-15.94153 0.07669 0.01589
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 1378
Residual Deviance: 1162 AIC: 1168
$outcome
$outcome$Combined
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) Ch K A Ch:A K:A
-15.6048 -0.2035 12.2849 -61.0979 0.5048 -6.6099 As for DynTxRegime::
is(object = fitObj$outcome$Combined)[1] "lm" "oldClass"is(object = fitObj$propensity)[1] "glm" "lm" "oldClass"As such, these objects can be passed to any tool defined for these classes. For example, the methods available for the object returned by the propensity score regression are
utils::methods(class = is(object = fitObj$propensity)[1L]) [1] add1 anova coerce confint cooks.distance deviance drop1 effects
[9] extractAIC family formula influence initialize logLik model.frame nobs
[17] predict print residuals rstandard rstudent show slotsFromS3 summary
[25] vcov weights
see '?methods' for accessing help and source codeSo, to plot the residuals
graphics::plot(x = residuals(object = fitObj$propensity))
Or, to retrieve the variance-covariance matrix of the parameters
stats::vcov(object = fitObj$propensity) (Intercept) SBP0 Ch
(Intercept) 1.689875691 -8.970374e-03 -1.095841e-03
SBP0 -0.008970374 5.178554e-05 2.752417e-06
Ch -0.001095841 2.752417e-06 3.072313e-06The methods DynTxRegime::
DynTxRegime::outcome(object = result)$Combined
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) Ch K A Ch:A K:A
-15.6048 -0.2035 12.2849 -61.0979 0.5048 -6.6099 DynTxRegime::propen(object = result)
Call: glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Coefficients:
(Intercept) SBP0 Ch
-15.94153 0.07669 0.01589
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 1378
Residual Deviance: 1162 AIC: 1168DynTxRegime::genetic(object = result)$value
[1] 13.14356
$par
[1] -0.92419308 0.01204358 -0.27660824
$gradients
[1] NA NA NA
$generations
[1] 19
$peakgeneration
[1] 8
$popsize
[1] 1000
$operators
[1] 122 125 125 125 125 126 125 126 0Once satisfied that the postulated models are suitable, the estimated optimal treatment regime, the recommended treatments, and the estimated value for the dataset used for the analysis can be retrieved.
The estimated optimal treatment regime is retrieved using function DynTxRegime::
DynTxRegime::regimeCoef(object = result) eta11 eta12 eta13
-0.92419308 0.01204358 -0.27660824 Function DynTxRegime::
DynTxRegime::optTx(x = result)$optimalTx
[1] 1 0 1 1 1 1 1 0 1 1 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1
[60] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 0 1
[119] 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1
[178] 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 0 1 1 1 0 0 1 0 1 1 0 1 1 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1
[237] 1 1 1 0 1 0 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1
[296] 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1
[355] 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 0 0 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1
[414] 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1
[473] 0 1 1 1 0 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 1 0 0 1 1 0 1 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0
[532] 0 1 1 1 0 1 1 1 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 0 1
[591] 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 0 1 1 1 1 1 0 1 0 1 0 0 1 1 0 0 1 1 1 1 1 0 1 0 0 1 1 1 1 1
[650] 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1
[709] 1 1 1 1 1 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 1 0 1 1 0 1 1 0 1 0 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 1 0 0 0 1 1 1 1
[768] 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 0 0 1 1 0 1 0 1 1 1 1 0 1 0 1 0 0
[827] 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1
[886] 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 1 0 1 1 1 1 1 1 0 1 0 1 0 0 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1
[945] 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 1 0 1 0 0 0 1 1 1 1
$decisionFunc
[1] NAThe object returned is a list. Element $optimalTx corresponds to the \(\widehat{d}^{opt}_{\eta}(H_{1i}; \widehat{\eta}_{1})\); element $decisionFunc is NA as it is not defined in this context but is included for continuity across methods.
Function DynTxRegime::
DynTxRegime::estimator(x = result)[1] 13.14356Function DynTxRegime::
The first new patient has the following baseline covariates
print(x = patient1) SBP0 W K Cr Ch
1 162 72.6 4.2 0.8 209.2The recommended treatment based on the previous analysis is obtained by providing the object returned by DynTxRegime::
DynTxRegime::optTx(x = result, newdata = patient1)$optimalTx
[1] 1
$decisionFunc
[1] NATreatment A= 1 is recommended.
The second new patient has the following baseline covariates
print(x = patient2) SBP0 W K Cr Ch
1 153 68.2 4.5 0.8 178.8And the recommended treatment is obtained by calling
DynTxRegime::optTx(x = result, newdata = patient2)$optimalTx
[1] 0
$decisionFunc
[1] NATreatment A= 0 is recommended.
Comparison of Estimators
The table below compares the estimated values and regime parameters for all of the estimators discussed here and under all the models considered in this chapter.
| (mmHg) | \(\widehat{\mathcal{V}}_{IPW}\) | \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) |
| \(\widehat{\mathcal{V}}_{Q}\) | — | 14.26 | 13.16 | 13.22 |
| \(\pi^{1}_{1}(h_{1};\gamma_{1})\) | 16.95 | 16.05 | 13.26 | 13.13 |
| \(\pi^{2}_{1}(h_{1};\gamma_{1})\) | 13.23 | 13.21 | 13.20 | 13.13 |
| \(\pi^{3}_{1}(h_{1};\gamma_{1})\) | 13.09 | 13.19 | 13.19 | 13.14 |
| (\(\widehat{\eta}_{1},\widehat{\eta}_{2},\widehat{\eta}_{3}\)) | IPW | \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) |
| Q | — | — | — | (-0.99, 0.01, -0.11) |
| \(\pi^{1}_{1}(h_{1};\gamma_{1})\) | (-0.38, 0.02, -0.87) | (-0.80, 0.02, -0.60) | (-0.97, 0.01, -0.23) | (-0.97, 0.01, -0.23) |
| \(\pi^{2}_{1}(h_{1};\gamma_{1})\) | (-1.00, 0.01, -0.20) | (-0.79, 0.02, -0.62) | (-0.98, 0.01, -0.21) | (-0.97, 0.01, -0.22) |
| \(\pi^{3}_{1}(h_{1};\gamma_{1})\) | (-0.38, 0.02, -0.87) | (-0.83, 0.02, -0.55) | (-0.97, 0.01, -0.22) | (-0.96, 0.01, -0.29) |
We have carried out a simulation study to evaluate the performances of the presented methods. We generated 1000 Monte Carlo data sets, each with \(n=1000\). The table below compares the Monte Carlo average estimated value and standard deviation of the estimated value. In addition, the Monte Carlo average of the standard errors as defined previously for each estimator. Using a Monte Carlo simulation with \(10^6\) replicates, we obtained \(\mathcal{V}(d^{opt}) = 13.46\).
| (mmHg) | \(\widehat{\mathcal{V}}_{IPW}(d)\) | \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) |
| \(\widehat{\mathcal{V}}_{Q}(d)\) | --- | 14.98 (0.65) | 13.43 (0.37) | 13.45 (0.36) |
| \(\pi^{1}_{1}(h_{1};\gamma_{1})\) | 17.58 (0.63) | 16.63 (0.54) | 13.54 (0.38) | 13.45 (0.37) |
| \(\pi^{2}_{1}(h_{1};\gamma_{1})\) | 13.46 (0.38) | 13.52 (0.43) | 13.46 (0.39) | 13.45 (0.37) |
| \(\pi^{3}_{1}(h_{1};\gamma_{1})\) | 13.47 (0.40) | 13.57 (0.44) | 13.46 (0.39) | 13.45 (0.37) |
Below, we compare the Monte Carlo average of the estimated parameters for the optimal treatment regime. For the outcome regression method we have excluded the estimated regimes under models \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) and \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) as the treatment regime of a different form. Recall that the
\[ \begin{align} d^{opt}_{1}(h_{1}) &= \text{I} (-65.0 + 0.5 \text{Ch} - 5.5 \text{K} > 0) \\ &= \text{I} (-0.996 + 0.008 \text{Ch} - 0.084 \text{K} > 0) \\ \end{align} \] where we have normalized the parameters to 1 in the second expression. In the Monte Carlo, parameters were normalized to 1 at each iteration; the MC average of the parameters is not normalized.
| (\(\widehat{\eta}_{1},\widehat{\eta}_{2},\widehat{\eta}_{3}\)) | \(\widehat{\mathcal{V}}_{IPW}(d)\) | \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) | \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) |
| \(\widehat{\mathcal{V}}_{Q}(d)\) | --- | --- | --- | (-0.996, 0.008,-0.085) |
| \(\pi^{1}_{1}(h_{1};\gamma_{1})\) | (-0.700, 0.018,-0.600) | (-0.440, 0.022,-0.747) | (-0.770, 0.017,-0.541) | (-0.894, 0.013,-0.349) |
| \(\pi^{2}_{1}(h_{1};\gamma_{1})\) | (-0.800, 0.016,-0.478) | (-0.672, 0.018,-0.577) | (-0.850, 0.016,-0.423) | (-0.892, 0.014,-0.353) |
| \(\pi^{3}_{1}(h_{1};\gamma_{1})\) | (-0.780, 0.017,-0.505) | (-0.626, 0.019,-0.607) | (-0.829, 0.015,-0.444) | (-0.885, 0.014,-0.371) |
\(Q_{1}(h_{1}, a_{1};\beta_{1})\)
Throughout Chapters 2-4, we consider three outcome regression models selected to represent a range of model (mis)specification. Note that we are not demonstrating a definitive analysis that one might do in practice, in which the analyst would use all sorts of variable selection techniques, etc., to arrive at a posited model. Rather, our objective is to illustrate how the methods work under a range of model (mis)specification.
Click on each tab below to see the model and basic model diagnostic steps. Note that this information was discussed previously in Chapter 2 and is repeated here for convenience.
The first model is a completely misspecified model
\[ Q^{1}_{1}(h_{1},a_{1};\beta_{1}) = \beta_{10} + \beta_{11} \text{W} + \beta_{12} \text{Cr} + a_{1}~(\beta_{13} + \beta_{14} \text{Cr}). \]
Modeling Object
The parameters of this model will be estimated using ordinary least squares via
The modeling objects for this regression step is
q1 <- modelObj::buildModelObj(model = ~ W + A*Cr,
solver.method = 'lm',
predict.method = 'predict.lm')Model Diagnostics
Though ultimately, the regression steps will be performed within the implementations of the treatment effect and value estimators, we make use of modelObj::
For \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) the regression can be completed as follows
OR1 <- modelObj::fit(object = q1, data = dataSBP, response = y)
OR1 <- modelObj::fitObject(object = OR1)
OR1
Call:
lm(formula = YinternalY ~ W + A + Cr + A:Cr, data = data)
Coefficients:
(Intercept) W A Cr A:Cr
-6.66893 0.02784 16.46653 0.56324 2.41004 where for convenience we have made use of modelObj’s
Let’s examine the regression results for the model under consideration. First, the diagnostic plots defined for “lm” objects.
par(mfrow = c(2,2))
graphics::plot(x = OR1)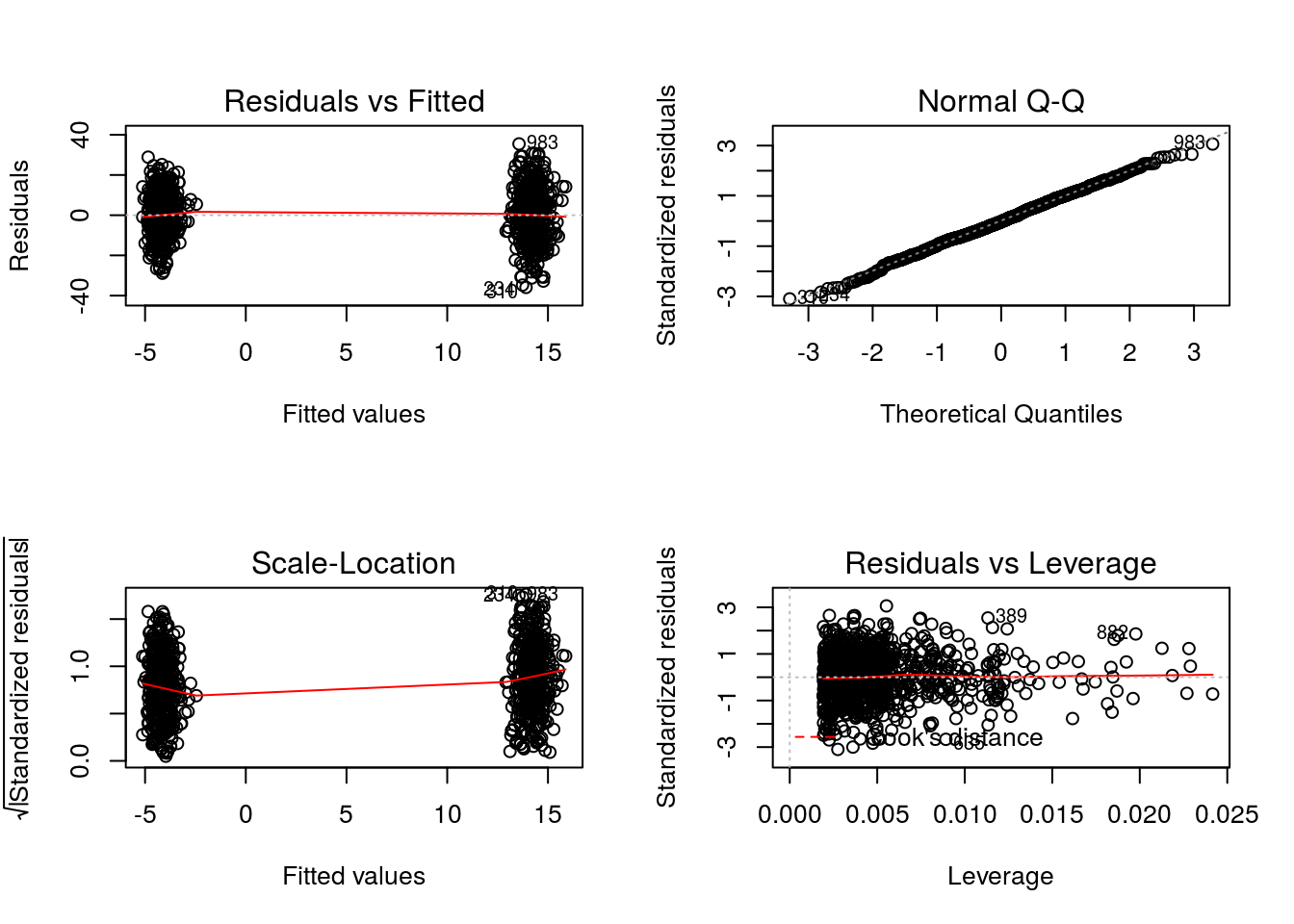
We see that the diagnostic plots for model \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) show some unusual behaviors. The two groupings of residuals in the Residuals vs Fitted and the Scale-Location plots are reflecting the fact that the model includes only the covariates W and Cr, neither of which are associated with outcome in the true regression relationship. Thus, for all practical purposes the model is fitting the two treatment means.
Now, let’s examine the summary statistics for the regression step
summary(object = OR1)
Call:
lm(formula = YinternalY ~ W + A + Cr + A:Cr, data = data)
Residuals:
Min 1Q Median 3Q Max
-35.911 -7.605 -0.380 7.963 35.437
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.66893 4.67330 -1.427 0.15389
W 0.02784 0.02717 1.025 0.30564
A 16.46653 5.96413 2.761 0.00587 **
Cr 0.56324 5.07604 0.111 0.91167
A:Cr 2.41004 7.22827 0.333 0.73889
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 11.6 on 995 degrees of freedom
Multiple R-squared: 0.3853, Adjusted R-squared: 0.3828
F-statistic: 155.9 on 4 and 995 DF, p-value: < 2.2e-16We see that the residual standard error is large and that the adjusted R-squared value is small.
Readers familiar with R might have noticed that the response variable specified in the call to the regression method is
The second model is an incomplete model having only one of the covariates of the true model,
\[ Q^{2}_{1}(h_{1},a_{1};\beta_{1}) = \beta_{10} + \beta_{11} \text{Ch} + a_{1}~(\beta_{12} + \beta_{13} \text{Ch}). \]
Modeling Object
As for \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\), the parameters of this model will be estimated using ordinary least squares via
The modeling object for this regression step is
q2 <- modelObj::buildModelObj(model = ~ Ch*A,
solver.method = 'lm',
predict.method = 'predict.lm')Model Diagnostics
For \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) the regression can be completed as follows
OR2 <- modelObj::fit(object = q2, data = dataSBP, response = y)
OR2 <- modelObj::fitObject(object = OR2)
OR2
Call:
lm(formula = YinternalY ~ Ch + A + Ch:A, data = data)
Coefficients:
(Intercept) Ch A Ch:A
36.5101 -0.2052 -89.5245 0.5074 where for convenience we have made use of modelObj’s
First, let’s examine the diagnostic plots defined for “lm” objects.
par(mfrow = c(2,4))
graphics::plot(x = OR2)
graphics::plot(x = OR1)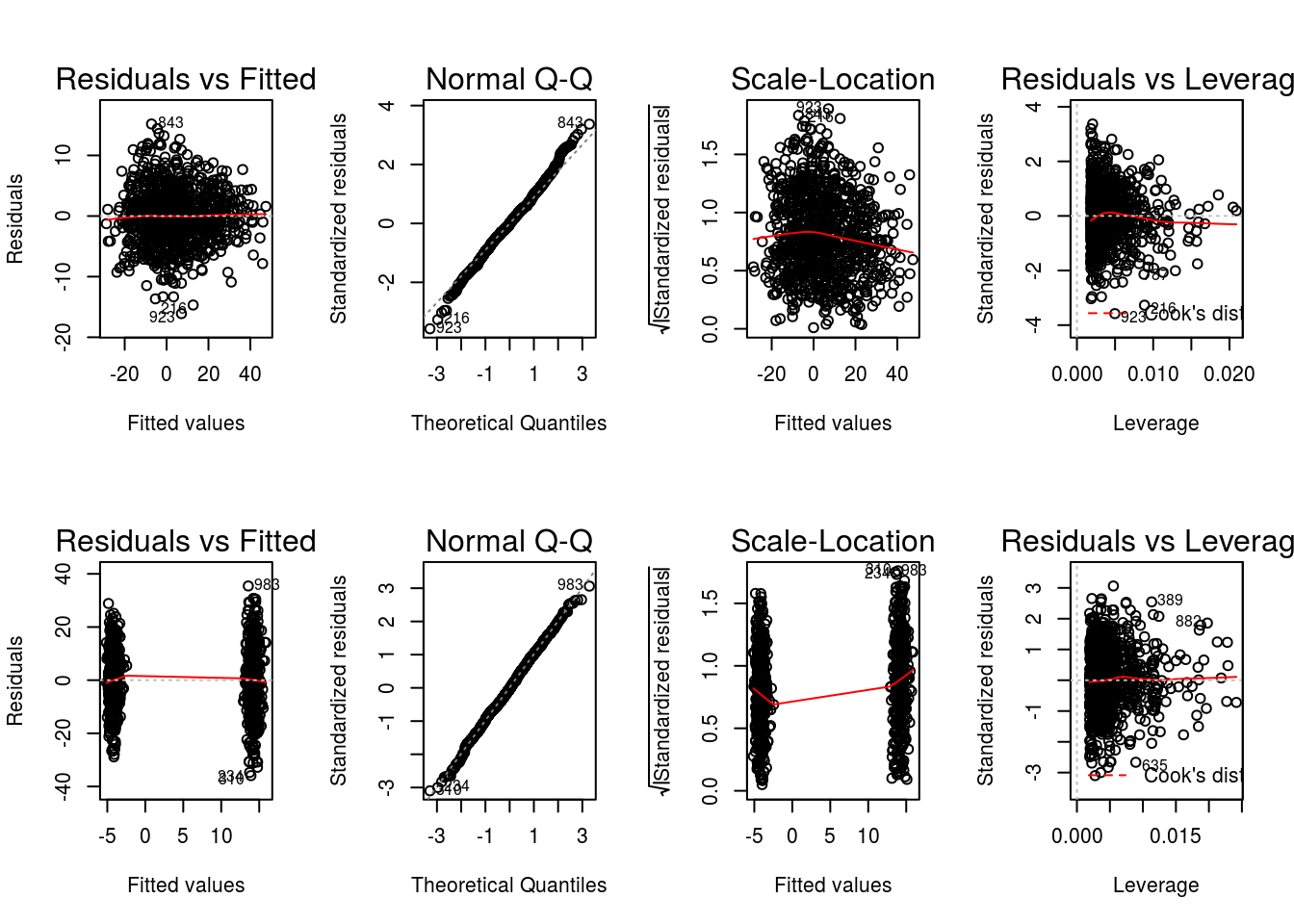
where we have included the diagnostic plots for model \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) for easy comparison. We see that the residuals from the fit of model \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) do not exhibit the two groupings, reflecting the fact that \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) is only partially misspecified in that it includes the important covariate Ch.
Now, let’s examine the summary statistics for the regression step
summary(object = OR2)
Call:
lm(formula = YinternalY ~ Ch + A + Ch:A, data = data)
Residuals:
Min 1Q Median 3Q Max
-16.1012 -2.7476 -0.0032 2.6727 15.1825
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.510110 0.933019 39.13 <2e-16 ***
Ch -0.205226 0.004606 -44.56 <2e-16 ***
A -89.524507 1.471905 -60.82 <2e-16 ***
Ch:A 0.507374 0.006818 74.42 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.511 on 996 degrees of freedom
Multiple R-squared: 0.907, Adjusted R-squared: 0.9068
F-statistic: 3239 on 3 and 996 DF, p-value: < 2.2e-16Comparing to the diagnostics for model \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\), we see that the residual standard error is smaller (4.51 vs 11.6) and that the adjusted R-squared value is larger (0.91 vs 0.38). Both of these results indicate that model \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) is a more suitable model for \(E(Y|X=x,A=a)\) than model \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\).
The third model we will consider is the correctly specified model used to generate the dataset,
\[ Q^{3}_{1}(h_{1},a_{1};\beta_{1}) = \beta_{10} + \beta_{11} \text{Ch} + \beta_{12} \text{K} + a_{1}~(\beta_{13} + \beta_{14} \text{Ch} + \beta_{15} \text{K}). \]
Modeling Object
As for \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) and \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\), the parameters of this model will be estimated using ordinary least squares via
The modeling object for this regression step is
q3 <- modelObj::buildModelObj(model = ~ (Ch + K)*A,
solver.method = 'lm',
predict.method = 'predict.lm')Model Diagnostics
For \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) the regression can be completed as follows
OR3 <- modelObj::fit(object = q3, data = dataSBP, response = y)
OR3 <- modelObj::fitObject(object = OR3)
OR3
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Coefficients:
(Intercept) Ch K A Ch:A K:A
-15.6048 -0.2035 12.2849 -61.0979 0.5048 -6.6099 where for convenience we have made use of modelObj’s
Again, let’s start by examining the diagnostic plots defined for “lm” objects.
par(mfrow = c(2,4))
graphics::plot(x = OR3)
graphics::plot(x = OR2)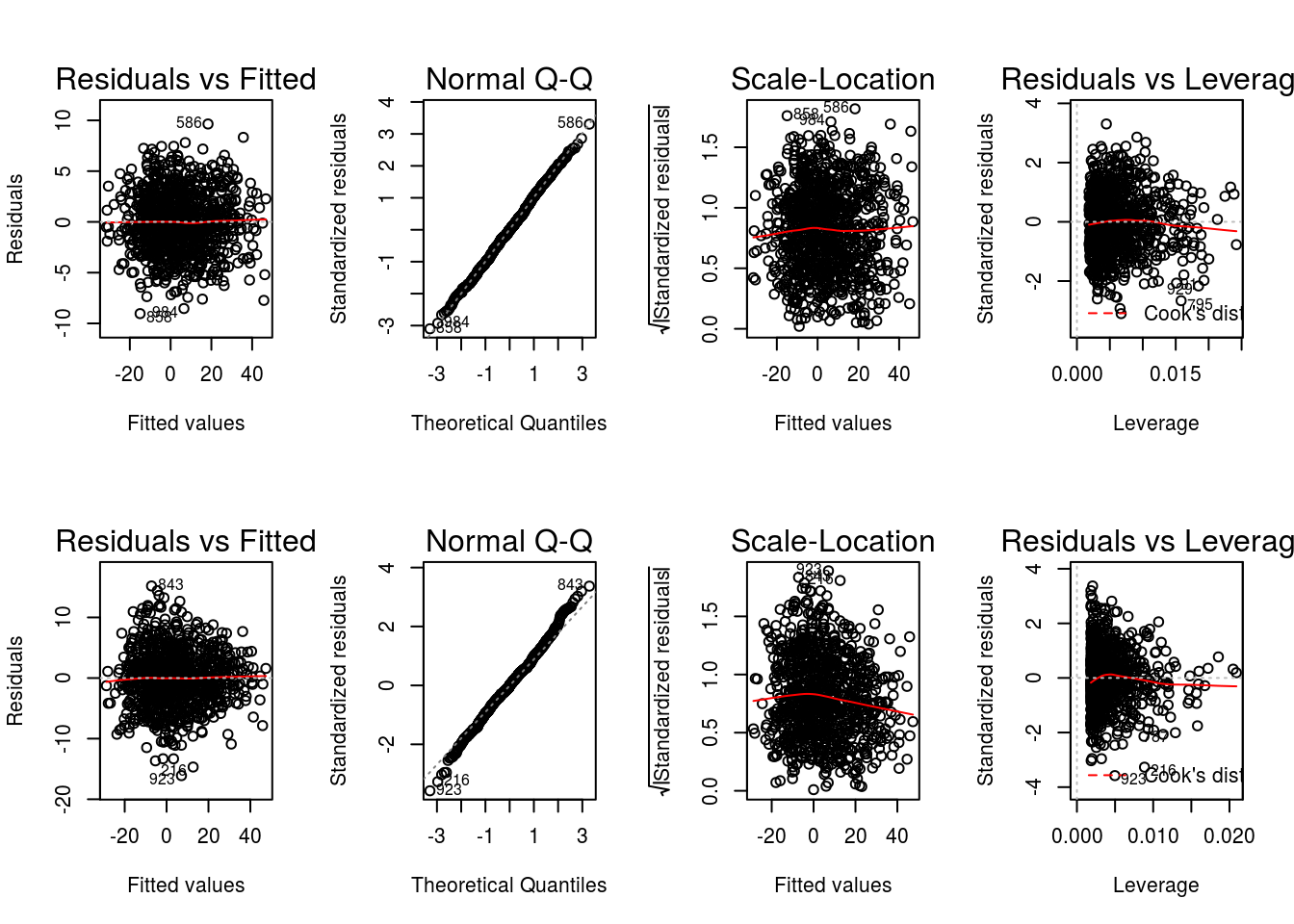
where we have included the diagnostic plots for model \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) for easy comparison. We see that the results for models \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\) and \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) are very similar, with model \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) yielding slightly better diagnostics (e.g., smaller residuals); a result in line with the knowledge that \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) is the model used to generate the data.
Now, let’s examine the summary statistics for the regression step
summary(object = OR3)
Call:
lm(formula = YinternalY ~ Ch + K + A + Ch:A + K:A, data = data)
Residuals:
Min 1Q Median 3Q Max
-9.0371 -1.9376 0.0051 2.0127 9.6452
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -15.604845 1.636349 -9.536 <2e-16 ***
Ch -0.203472 0.002987 -68.116 <2e-16 ***
K 12.284852 0.358393 34.278 <2e-16 ***
A -61.097909 2.456637 -24.871 <2e-16 ***
Ch:A 0.504816 0.004422 114.168 <2e-16 ***
K:A -6.609876 0.538386 -12.277 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.925 on 994 degrees of freedom
Multiple R-squared: 0.961, Adjusted R-squared: 0.9608
F-statistic: 4897 on 5 and 994 DF, p-value: < 2.2e-16As for model \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\), we see that the residual standard error is smaller (2.93 vs 4.51) and that the adjusted R-squared value is larger (0.96 vs 0.91). Again, these results indicate that model \(Q^{3}_{1}(h_{1},a_{1};\beta_{1})\) is a more suitable model than both models \(Q^{1}_{1}(h_{1},a_{1};\beta_{1})\) and \(Q^{2}_{1}(h_{1},a_{1};\beta_{1})\).
\(\pi_{1}(h_{1};\gamma_{1})\)
Throughout Chapters 2-4, we consider three propensity score models selected to represent a range of model (mis)specification. Note that we are not demonstrating a definitive analysis that one might do in practice, in which the analyst would use all sorts of variable selection techniques, etc., to arrive at a posited model. Our objective is to illustrate how the methods work under a range of model (mis)specification.
Click on each tab below to see the model and basic model diagnostic steps. Note that this information was discussed previously in Chapter 2 and is repeated here for convenience.
The first model is a completely misspecified model having none of the covariates used in the data generating model
\[ \pi^{1}_{1}(h_{1};\gamma_{1}) = \frac{\exp(\gamma_{10} + \gamma_{11}~\text{W} + \gamma_{12}~\text{Cr})}{1+\exp(\gamma_{10} + \gamma_{11}~\text{W} + \gamma_{12}~\text{Cr})}. \]
Modeling Object
The parameters of this model will be estimated using maximum likelihood via
p1 <- modelObj::buildModelObj(model = ~ W + Cr,
solver.method = 'glm',
solver.args = list(family='binomial'),
predict.method = 'predict.glm',
predict.args = list(type='response'))Model Diagnostics
Though we will implement our treatment effect and value estimators in such a way that the regression step is performed internally, it is convenient to do model diagnostics separately here. We will make use of modelObj::
For \(\pi^{1}_{1}(h_{1};\gamma_{1})\) the regression can be completed as follows:
PS1 <- modelObj::fit(object = p1, data = dataSBP, response = dataSBP$A)
PS1 <- modelObj::fitObject(object = PS1)
PS1
Call: glm(formula = YinternalY ~ W + Cr, family = "binomial", data = data)
Coefficients:
(Intercept) W Cr
0.966434 -0.007919 -0.703766
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 1378
Residual Deviance: 1374 AIC: 1380where for convenience we have made use of modelObj’s
Now, let’s examine the regression results for the model under consideration.
summary(object = PS1)
Call:
glm(formula = YinternalY ~ W + Cr, family = "binomial", data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.239 -1.104 -1.027 1.248 1.443
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.966434 0.624135 1.548 0.1215
W -0.007919 0.004731 -1.674 0.0942 .
Cr -0.703766 0.627430 -1.122 0.2620
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1377.8 on 999 degrees of freedom
Residual deviance: 1373.8 on 997 degrees of freedom
AIC: 1379.8
Number of Fisher Scoring iterations: 4First, in comparing the null deviance (1377.8) and the residual deviance (1373.8), we see that including the independent variables does not significantly reduce the deviance. Thus, this model is not significantly better than the constant propensity score model. However, we know that the data mimics an observational study for which the propensity score is not constant or known. And, note that the Akaike Information Criterion (AIC) is large (1379.772). Though the AIC value alone does not tell us much about the quality of our model, we can compare this to other models to determine a relative quality.
The second model is an incomplete model having only one of the covariates of the true data generating model
\[ \pi^{2}_{1}(h_{1};\gamma_{1}) = \frac{\exp(\gamma_{10} + \gamma_{11} \text{Ch})}{1+\exp(\gamma_{10} + \gamma_{11} \text{Ch})}. \]
Modeling Object
As for \(\pi_{1}(h_{1};\gamma)\) the parameters of this model will be estimated using maximum likelihood via
The modeling objects for this regression step is
p2 <- modelObj::buildModelObj(model = ~ Ch,
solver.method = 'glm',
solver.args = list(family='binomial'),
predict.method = 'predict.glm',
predict.args = list(type='response'))The regression is completed as follows:
PS2 <- modelObj::fit(object = p2, data = dataSBP, response = dataSBP$A)
PS2 <- modelObj::fitObject(object = PS2)
PS2
Call: glm(formula = YinternalY ~ Ch, family = "binomial", data = data)
Coefficients:
(Intercept) Ch
-3.06279 0.01368
Degrees of Freedom: 999 Total (i.e. Null); 998 Residual
Null Deviance: 1378
Residual Deviance: 1298 AIC: 1302Again, we use
summary(PS2)
Call:
glm(formula = YinternalY ~ Ch, family = "binomial", data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.7497 -1.0573 -0.7433 1.1449 1.9316
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.062786 0.348085 -8.799 <2e-16 ***
Ch 0.013683 0.001617 8.462 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1377.8 on 999 degrees of freedom
Residual deviance: 1298.2 on 998 degrees of freedom
AIC: 1302.2
Number of Fisher Scoring iterations: 4First, in comparing the null deviance (1377.8) and the residual deviance (1298.2), we see that including the independent variables leads to a smaller deviance than obtained from the intercept only model. And finally, we see that the AIC is large (1302.247), but it is less than that obtained for \(\pi^{1}_{1}(h_{1};\gamma_{1})\) (1379.772). This result is not unexpected as we know that the model is only partially misspecified.
The third model we will consider is the correctly specified model used to generate the data set,
\[ \pi^{3}_{1}(h_{1};\gamma_{1}) = \frac{\exp(\gamma_{10} + \gamma_{11}~\text{SBP0} + \gamma_{12}~\text{Ch})}{1+\exp(\gamma_{10} + \gamma_{11}~\text{SBP0}+ \gamma_{12}~\text{Ch})}. \]
The parameters of this model will be estimated using maximum likelihood via
The modeling objects for this regression step is
p3 <- modelObj::buildModelObj(model = ~ SBP0 + Ch,
solver.method = 'glm',
solver.args = list(family='binomial'),
predict.method = 'predict.glm',
predict.args = list(type='response'))The regression is completed as follows:
PS3 <- modelObj::fit(object = p3, data = dataSBP, response = dataSBP$A)
PS3 <- modelObj::fitObject(object = PS3)
PS3
Call: glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Coefficients:
(Intercept) SBP0 Ch
-15.94153 0.07669 0.01589
Degrees of Freedom: 999 Total (i.e. Null); 997 Residual
Null Deviance: 1378
Residual Deviance: 1162 AIC: 1168Again, we use
summary(PS3)
Call:
glm(formula = YinternalY ~ SBP0 + Ch, family = "binomial", data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3891 -0.9502 -0.4940 0.9939 2.1427
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -15.941527 1.299952 -12.263 <2e-16 ***
SBP0 0.076687 0.007196 10.657 <2e-16 ***
Ch 0.015892 0.001753 9.066 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1377.8 on 999 degrees of freedom
Residual deviance: 1161.6 on 997 degrees of freedom
AIC: 1167.6
Number of Fisher Scoring iterations: 3First, we see from the null deviance (1377.8) and the residual deviance (1161.6) that including the independent variables does reduce the deviance as compared to the intercept only model. And finally, we see that the AIC is large (1167.621), but it is less than that obtained for both \(\pi^{1}_{1}(h_{1};\gamma_{1})\) (1379.772) and \(\pi^{2}_{1}(h_{1};\gamma_{1})\) (1302.247). This result is in-line with the knowledge that this is the data generating model.
