Description
We explore the estimators introduced in Chapters 6 and 7 using a simulated data set adapted from the \(K=3\) scenario in Zhang, et al., 2013. Specifically, the scenario mimics a multiple decision point study in which HIV-infected patients receive one of two treatment options at the first decision point, coded as \(\{0,1\}\). Subsequent treatments are as follows: if the preceding treatment was 1, continue treatment 1, otherwise receive one of two treatment options coded as \(\{0,1\}\).
The data set depicts a three-decision-point study. The primary end point of interest is a continuous variable, the 18-month CD4 count, for which larger values are preferred.
The dataset comprises one thousand patients (\(n=1000\)). The baseline patient characteristic is the baseline CD4 count \(\text{CD4_0}\) (cells/mm\(^3\)). At Decision 1, each patient in this study received one of two treatments (\(A_{1} \in \{0,1\}\)). Six-months after the first treatment decision, the CD4 count was reassessed, and a second treatment decision was made. Specifically, covariates \(\text{CD4_6}\) (cells/mm\(^3\)) was measured, and if \(A_{1} = 0\), one of two treatments (\(A_{2} \in \{0,1\}\)) was assigned; if \(A_{1} = 1\), \(A_{2} = 1\). Six months later, 12-months after the first treatment, the patient’s CD4 count was remeasured, \(\text{CD4_12}\) (cells/mm\(^3\)), and a final treatment decision was made; if \(A_{2} = 0\), one of two treatments (\(A_{3} \in \{0,1\}\)) was assigned; if \(A_{2} = 1\), \(A_{3} = 1\). Finally, six months later, 18-months after the initial treatment, the patient’s CD4 count is remeasured; this is the outcome of interest, \(Y\) (cells/mm\(^3\)), for which higher values are more desirable. The observed data are independent and identically distributed
\[ \{\text{CD4_0}_{i}, A_{1i}, \text{CD4_6}_{i}, A_{2i}, \text{CD4_12}_{i}, A_{3i}, Y_i\},~ \text{for}~ i = 1, \dots, n. \]
The primary outcome of interest is \(Y\), where larger values are considered better. We assume that all participants adhered to the treatment plan to which they were assigned and that no participants dropped out of the study.
For the simulation scenario used to generate the data, the true value under the optimal regime is \(\mathcal{V}(d^{opt}) = 1120\) cells/mm\(^3\) and the optimal regime is
\[ \begin{align} d^{opt}_{1}(h_{1}) &= \text{I} (\text{CD4_0} < 250 ~ \text{cells/mm}^3) \\ d^{opt}_{2}(h_{2}) &= d_{1}(h_{1}) + \{1 - d_{1}(h_{1})\} \text{I} (\text{CD4_6} < 360 ~ \text{cells/mm}^3) \\ d^{opt}_{3}(h_{3}) &= d_{2}(h_{2}) + \{1 - d_{2}(h_{2})\} \text{I} (\text{CD4_12} < 300 ~ \text{cells/mm}^3) \end{align} \]
This scenario implies the following true outcome regression relationship
\[ \begin{align} Q_{3}(h_{3},a_{3}) =& 400 + 1.6~\text{CD4_0} \\ &- |500 - 2~\text{CD4_0}| \{a_{1} - \text{I}(250 - \text{CD4_0} > 0.0)\}^2 \\ &- (1-a_{1})|720 - 2~\text{CD4_6}|\{a_{2} - \text{I}(360 - \text{CD4_6} > 0.0)\}^2 \\ &- (1-a_{2})|600 - 2~\text{CD4_12}|\{a_{3} - \text{I}(300 - \text{CD4_12} > 0.0)\}^2 \end{align} \]
and propensity models
\[ \omega_1(h_{1},1) = \frac{\exp(2 - 0.006~\text{CD4_0})}{1+\exp(2 - 0.006~\text{CD4_0})}, \] \[ \omega_{2,2}(h_{2},1) = \frac{\exp(0.8 - 0.004~\text{CD4_6})}{1+\exp(0.8 - 0.004~\text{CD4_6})}, \]
and
\[ \omega_{3,2}(h_{3},1) = \frac{\exp(1.0 - 0.004~\text{CD4_12})}{1+\exp(1.0 - 0.004~\text{CD4_12})}. \]
Once downloaded, the data set can be loaded into R using
dataMDPF <- utils::read.csv(file = 'path_to_file/dataMDP_feasible.txt', header = TRUE)where ‘path_to_file’ is the full path to the downloaded data set file.
Examine the first few records of the data set
utils::head(x = dataMDPF) CD4_0 A1 CD4_6 A2 CD4_12 A3 Y
1 329.2934 1 425.9694 1 348.6091 1 811
2 477.7429 0 586.2623 0 465.0529 0 1181
3 558.4441 0 692.3956 0 562.4883 0 1288
4 215.4302 1 264.8375 1 202.2302 1 769
5 492.9125 0 613.6599 0 499.1023 1 744
6 500.6056 0 622.7476 0 509.5678 1 852to ensure that the data set contains the expected covariates.
Simulation Scenario
The data for this simulated trial were generated from the following models:
set.seed(seed = 1234L)
n <- 1000L\[ \text{CD4_0} \sim \mathcal{N}(\mu=450, \sigma^2=100^2). \]
CD4_0 <- stats::rnorm(n = n, mean = 450.0, sd = 100.0)\[ A_{1} \sim B\{n=1, p= \omega_{1}(h_{1})\} \]
where
\[ \omega_{1}(h_{1}) = \text{expit}(2 - 0.006~\text{CD4_0}) \]
and \(\text{expit}(u) = e^{u}/(1+e^{u})\).
xb <- 2.0 - 0.006*CD4_0
probA1 <- exp(x = xb) / {1.0 + exp(x = xb)}
A1 <- stats::rbinom(n = n, size = 1L, prob = probA1)\[ \text{CD4_6} \sim \mathcal{N}(\mu=1.25~\text{CD4_0}, \sigma^2=8^2). \]
CD4_6 <- stats::rnorm(n = n, mean = 1.25*CD4_0, sd = 8.0)\[ A_{2} \sim B\{n=1, p= \omega_2(h_{2})\} \]
where \[ \omega_{2}(h_{2}) = \text{I}\{s_{2}(h_{2})=1\}~\omega_{2,1}(h_{2},1) + \text{I}\{s_{2}(h_{2})=2\}~\omega_{2,2}(h_{2},a_{2}). \]
Recall, there are two distinct subsets of \(\mathcal{A}_2 = \{0, 1\}\) that are feasible sets \[ s_{2}(h_{2}) = \left\{\begin{array}{c} 1 \quad \text{if} ~ a_{1} = 1 \\ 2 \quad \text{if} ~ a_{1} = 0 \end{array} \right. \] with probability scores \[ \begin{align} \omega_{2,1}(h_{2},a_{2}) &= P(A_{2} = 1 | H_{2} = h_{2}) = 1 \\ \omega_{2,2}(h_{2},a_{2}) &= P(A_{2} = 1 | H_{2} = h_{2}) = \text{expit}(0.8 - 0.004~\text{CD4_6}), \\ \end{align} \]
where \(\text{expit}(u) = e^{u}/(1+e^{u})\).
xb <- 0.8 - 0.004*CD4_6
probA2 <- A1 + {1.0 - A1} * exp(x = xb) / {1.0 + exp(x = xb)}
A2 <- stats::rbinom(n = n, size = 1L, prob = probA2)\[ \text{CD4_12} \sim \mathcal{N}(\mu=0.8~\text{CD4_6}, \sigma^2=8^2). \]
CD4_12 <- stats::rnorm(n = n, mean = 0.8*CD4_6, sd = 8.0)\[ A_{3} \sim B\{n=1, p= \omega_{3}(h_{3})\} \]
where \[ \omega_{3}(h_{3}) = \text{I}\{s_{3}(h_{3})=1\}~\omega_{3,1}(h_{3},a_{3}) + \text{I}\{s_{3}(h_{3})=2\}~\omega_{3,2}(h_{3},a_{3}). \]
Recall, there are two distinct subsets of \(\mathcal{A}_3 = \{0, 1\}\) that are feasible sets \[ s_{3}(h_{3}) = \left\{\begin{array}{c} 1 \quad \text{if} ~ a_{2} = 1 \\ 2 \quad \text{if} ~ a_{2} = 0 \end{array} \right. \] with probability scores \[ \begin{align} \omega_{3,1}(h_{3},a_{3}) &= P(A_{3} = 1 | H_{3} = h_{3}) = 1 \\ \omega_{3,2}(h_{3},a_{3}) &= P(A_{3} = 1 | H_{3} = h_{3}) = \text{expit}(1.0 - 0.004~\text{CD4_12}), \\ \end{align} \]
where \(\text{expit}(u) = e^{u}/(1+e^{u})\).
xb <- 1.0 - 0.004*CD4_12
probA3 <- A2 + {1.0 - A2} * exp(x = xb) / {1.0 + exp(x = xb)}
A3 <- stats::rbinom(n = n, size = 1L, prob = probA3)\[ Y \sim \mathcal{N}(\mu=\mu, \sigma^2=60^2), \]
where \(0 \le Y \le 1500\) and
\[ \begin{align} \mu = & 400 + 1.6~X_{1} \\ & - \left|500 - 2.0~X_{1}\right|\{A_{1} - \text{I}(250-X_{1}>0)\}^2 \\ & - (1-A_{1})\left|720 - 2~X_{2}\right|\{A_{2} - \text{I}(360-X_{2}>0)\}^2 \\ & - (1-A_{2})\left|600 - 2~X_{3}\right|\{A_{3} - \text{I}(300-X_{3}>0)\}^2. \end{align} \]
mu <- 400.0 + 1.6*CD4_0 -
abs(x = {500.0 - 2.0*CD4_0})*{A1 - {250.0 - CD4_0 > 0.0}}^2 -
{1.0 - A1} * abs(x = {720.0 - 2.0*CD4_6})*{A2 - {360.0 - CD4_6 > 0.0}}^2 -
{1.0 - A2} * abs(x = {600.0 - 2.0*CD4_12})*{A3 - {300.0 - CD4_12 > 0.0}}^2
pY_L <- min(stats::pnorm(q = 0, mean = mu, sd = 60), 0.999)
pY_U <- stats::pnorm(q = 2000, mean = mu, sd = 60)
prob <- stats::runif(n = n, min = pY_L, max = pY_U)
Y <- stats::qnorm(p = prob, mean = mu, sd = 60)
Y <- round(x = Y, digit = 0L)From this, we see that the true optimal treatment regime is
\[ \begin{align} d^{opt}_{1}(h_{1}) &= \text{I} (\text{CD4_0} < 250 ~ \text{cells/mm}^3) \\ d^{opt}_{2}(h_{2}) &= d_{1}(h_{1}) + \{1 - d_{1}(h_{1})\} \text{I} (\text{CD4_6} < 360 ~ \text{cells/mm}^3) \\ d^{opt}_{3}(h_{3}) &= d_{2}(h_{2}) + \{1 - d_{2}(h_{2})\} \text{I} (\text{CD4_12} < 300 ~ \text{cells/mm}^3) \end{align} \]
and \(\mathcal{V}(d^{opt}) = 400 + 1.6 * 450 = 1120\) cells/mm\(^3\).
Summary
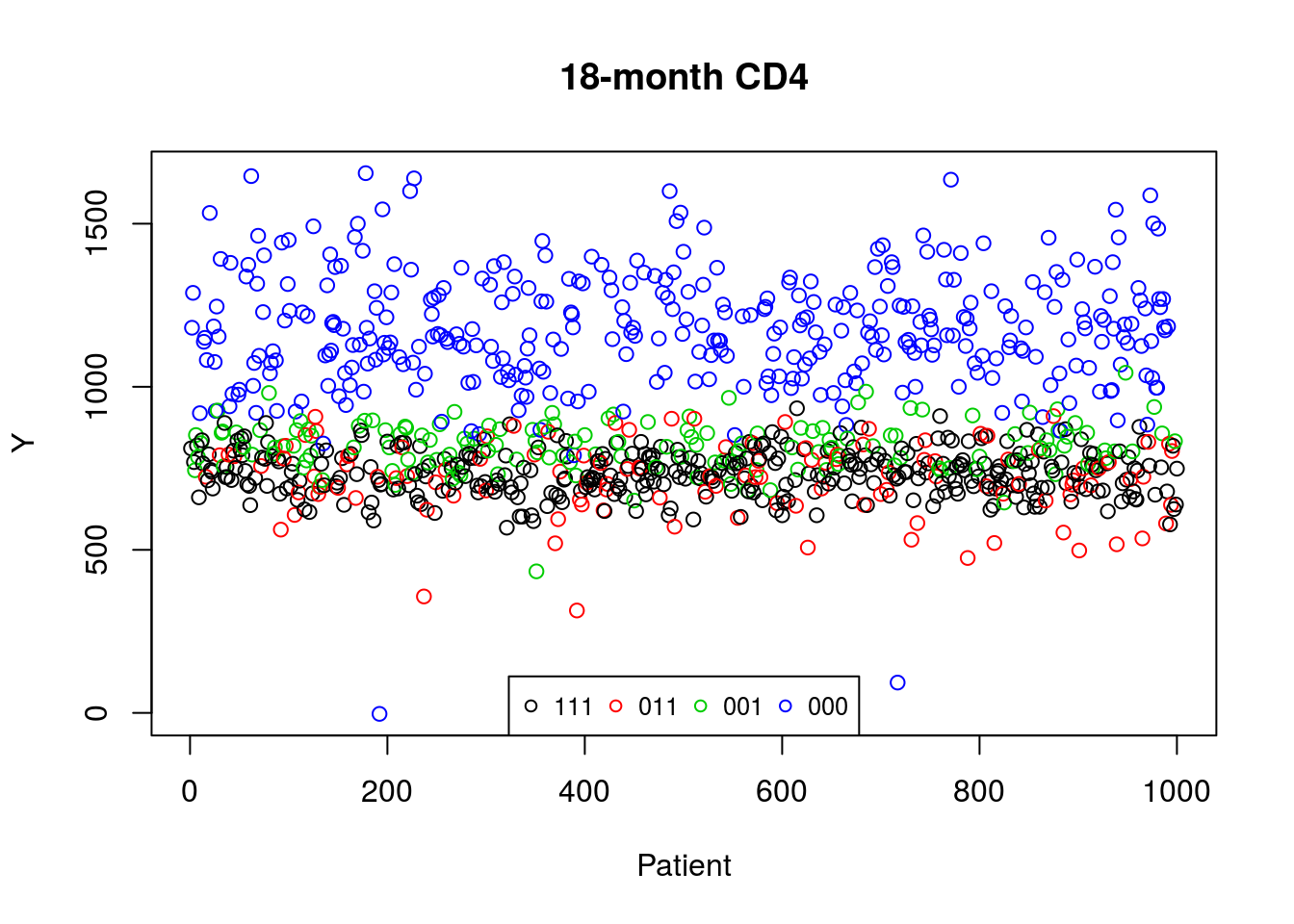
The outcome of interest, the 18-month CD4 count, is plotted below. Recall that we define the outcome of interest such that larger values are more desirable. The colors indicate the combination of treatments received across the three decision points.
The summary data for each covariate is given below.
summary(object = dataMDPF) CD4_0 A1 CD4_6 A2 CD4_12 A3 Y
Min. :110.4 Min. :0.000 Min. :140.9 Min. :0.000 Min. : 89.57 Min. :0.000 Min. : -3.0
1st Qu.:382.7 1st Qu.:0.000 1st Qu.:476.7 1st Qu.:0.000 1st Qu.:380.89 1st Qu.:0.000 1st Qu.: 727.5
Median :446.0 Median :0.000 Median :556.7 Median :0.000 Median :446.70 Median :1.000 Median : 819.0
Mean :447.3 Mean :0.368 Mean :559.4 Mean :0.486 Mean :447.45 Mean :0.637 Mean : 905.4
3rd Qu.:511.6 3rd Qu.:1.000 3rd Qu.:637.5 3rd Qu.:1.000 3rd Qu.:512.49 3rd Qu.:1.000 3rd Qu.:1095.2
Max. :769.6 Max. :1.000 Max. :955.7 Max. :1.000 Max. :771.55 Max. :1.000 Max. :1655.0 
